mybatis源码/mybatis执行流程源码解析

https://www.cnblogs.com/cxiaocai/tag/%E9%9D%A2%E8%AF%95%E9%A2%98/
public SqlSession session;
    public SqlSessionFactory sqlSessionFactory;

    @Before
    public void init() throws IOException {
        String resource = "mybatis-config.xml";
        InputStream inputStream = Resources.getResourceAsStream(resource);
        sqlSessionFactory = new SqlSessionFactoryBuilder().build(inputStream);
        session = sqlSessionFactory.openSession();
    }

    @Test
    public void studentTest() {
        StudentMapper mapper = session.getMapper(StudentMapper.class);
        StudentBean result = mapper.selectUser(1);
        System.out.println(result);
        session.commit();
    }

就是拿到流文件，
也是我们主配置文件，
进行流文件解析，
传入到build内，
构建成一个sqlSessionFactory，
再由sqlSessionFactory得到session，
拿到mapper，
执行sql，
完成。

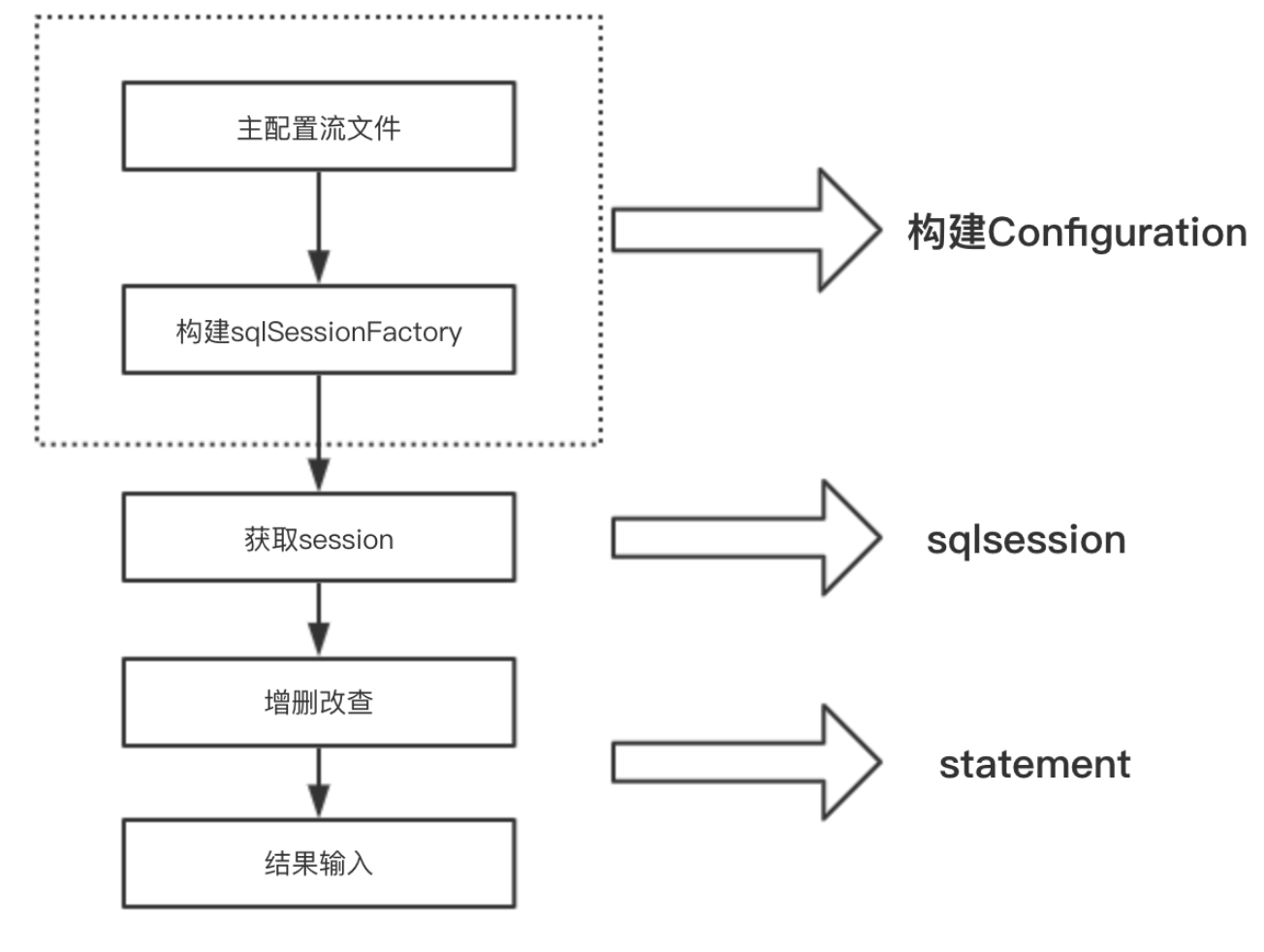
转变为我们的代码大概就是这三步，构建Configuration对象，构建我们的sqlsessionfactory，得到我们的session，得到对应的statement（处理参数和结果）从而得到结果集。

Configuration解析：

　　我们打开Configuration类可以看到，里面很多的属性设置，包括缓存，mapper，插件等等，其实就是把我们的xml标签转化为对象了，这里需要说明一下的是，这个解析过程是把所有的相关的xml都转为Configuration对象了，包括config.xml和mapper.xml。源码太多，我就不粘贴了。我给你看一下我转化完成的。

这里没有什么神秘的，就是一个xml解析的过程，在XMLConfigBuilder类的parse方法，生成了完成的Configuration对象，有兴趣的可以打个断点看一下。

这里要注意的就是里面很多元素是一个对应多个的，很多属性是map和set。顺便收一下里面是由多个构造器来构建的。

https://www.cnblogs.com/cxiaocai/p/11534137.html

总结一下就是：

1.拿到流文件config.xml和mapper.xml；

2.用我们的两个或多个流文件创建一个Configuration对象，（单一职责原则来构建的，很多个构造器来构建的，例如XMLConfigBuilder）

3.将Configuration对象塞给SqlSessionFactoryBuilder类的build方法，构建SqlSessionFactory对象。

4.sqlSessionFactory.openSession()拿到我们的session对象。

5.由session对象和Configuration对象封装参数和结果集映射，产生对应的执行器来，二级缓存执行器和BaseExecutor执行器。

6.由二级缓存执行器CachingExecutor来优先查询二级缓存是否存在，不存在执行BaseExecutor执行器的query或update方法。

7.拿到结果集转换ResultMap，session关闭，写入二级缓存，返回结束。