用matlab计算线性回归问题

看机器学习的时候遇到的第一个算法就是线性回归，高数中很详细的说明了线性回归的原理和最小2乘法的计算过程，很显然不适合手动计算，好在各种语言都有现成的函数使用，让我们愉快的做个调包侠吧

简单线性回归

R越接近1表示拟合效果越好

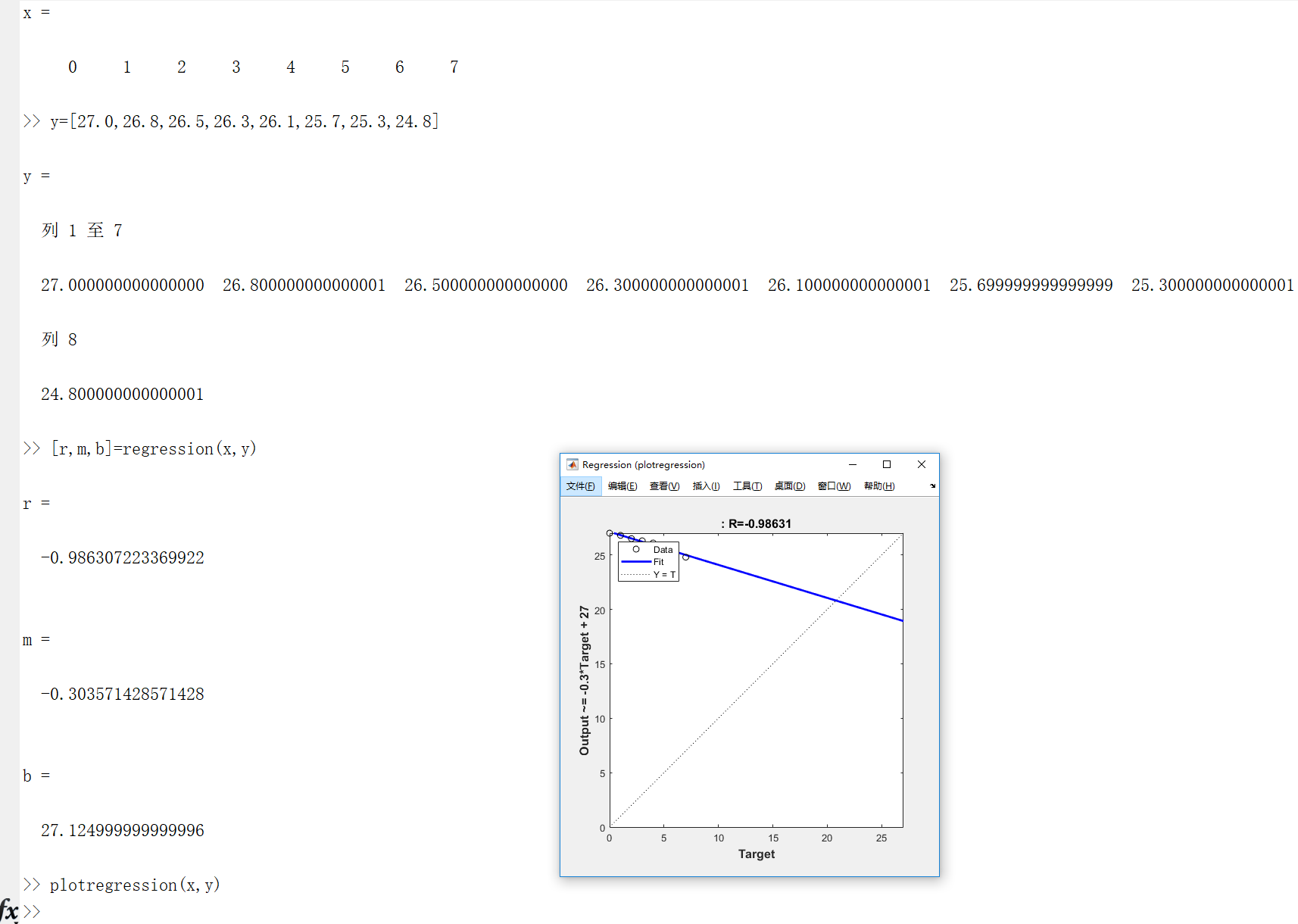
>> x=[0,1,2,3,4,5,6,7]

x =

     0     1     2     3     4     5     6     7

>> y=[27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8]

y =

  列 1 至 7

  27.000000000000000  26.800000000000001  26.500000000000000  26.300000000000001  26.100000000000001  25.699999999999999  25.300000000000001

  列 8

  24.800000000000001

>> [r,m,b]=regression(x,y)

r =

  -0.986307223369922

m =

  -0.303571428571428

b =

  27.124999999999996

>> plotregression(x,y)
>>

多元线性回归

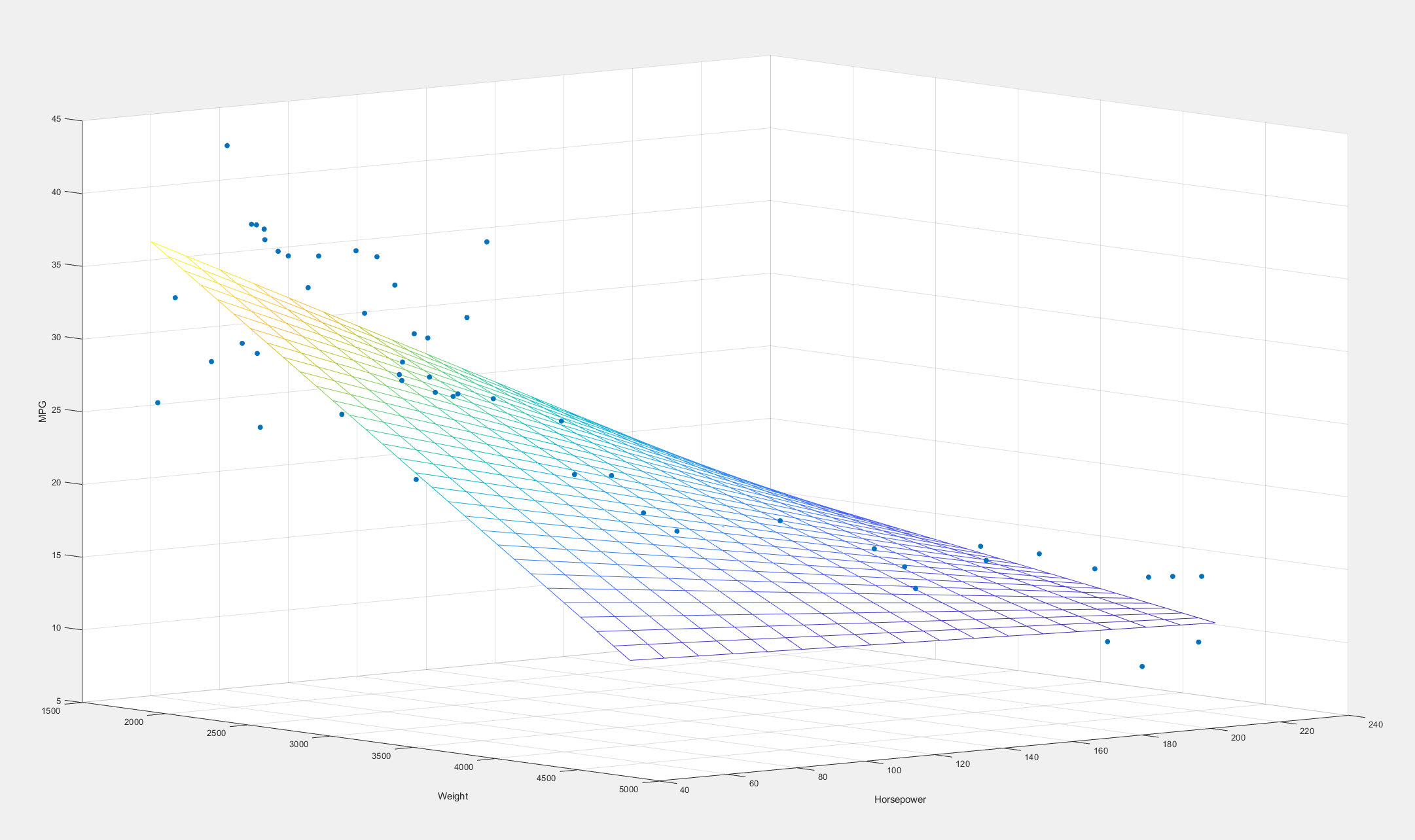
>> load carsmall
>> x1 = Weight;
>> x2 = Horsepower;
>> y = MPG;
>> X = [ones(size(x1)) x1 x2 x1.*x2];
>> b = regress(y,X)

b =

  60.710360805049135
  -0.010153547589001
  -0.188206440954574
   0.000038494827316

>> scatter3(x1,x2,y,'filled')
hold on
x1fit = min(x1):100:max(x1);
x2fit = min(x2):10:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT + b(4)*X1FIT.*X2FIT;
mesh(X1FIT,X2FIT,YFIT)
xlabel('Weight')
ylabel('Horsepower')
zlabel('MPG')
view(50,10)
hold off
>>