引入

上一篇写了二叉排序树，构建一个二叉排序树，如果构建序列是完全有序的，则会出现这样的情况：

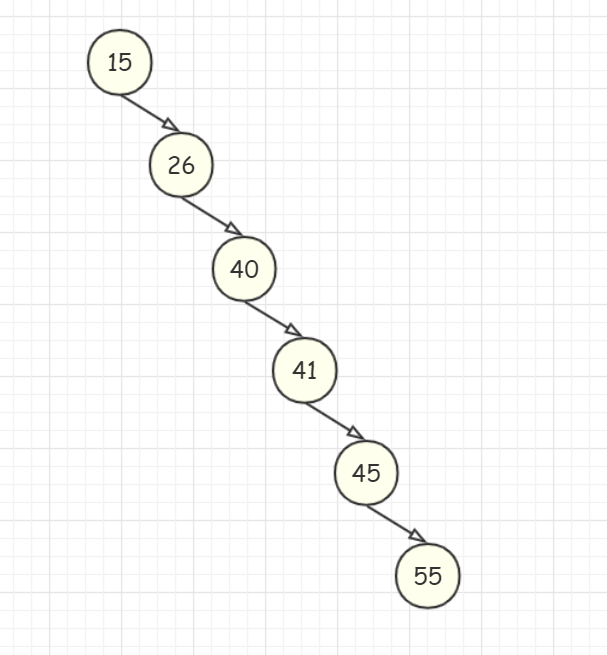
显然这种情况会使得二叉搜索树退化成链表。当出现这样的情况，二叉排序树的查找也就退化成了线性查找，所以我们需要合理调整二叉排序树的形态，使得树上的每个结点都尽量有两个子结点，这样整个二叉树的高度就会大约在\(log(n)\) 左右，其中 \(n\) 为结点个数。

基本性质

​ AVL树也称为平衡二叉树，是一种自平衡的二叉排序树，本质上仍然是一颗二叉排序树，只是增加了“平衡”的要求，平衡是指，对AVL树中任何节点的两个子树的高度之差（称为平衡因子）的绝对值不超过 \(1\) 。能保证上面这一点，AVL树的高度就能始终保持在 \(O(logn)\) 级别。

数据结构定义

由于需要对每个结点都得到平衡因子，因此在AVL树的结构中加入一个变量height，用来记录当前结点为根结点的子树的高度：

  1. typedef struct Node
  2. {
  3. 	char data;
  4.     int height;
  5. 	struct Node* Left;
  6. 	struct Node* Right;
  7. }*AVLTree;

获取 root 结点高度：

  1. int getHeight(Node *root){
  2. 	if(!root) return 0;//空节点高度为0
  3. 	return root->height;
  4. }

基本操作

查找

​ AVL树是一颗二叉查找树，因此查找操作与二叉查找树相同。因为AVL树的高度为 \(O(logn)\) 级别，所以查找操作的时间复杂度为 \(O(logn)\)。

可以得到和二叉查找树完全相同的代码：

  1. //找不到返回NULL，找到返回该节点。
  2. //非递归
  3. Node* Find(AVLTree t, int x) {
  4. 	if (!t)return NULL;
  5. 	if (t->data == x) return t;
  6. 	if (x < t->data) return BSTreeFind(t->Left, x);
  7. 	if (x > t->data) return BSTreeFind(t->Right, x);
  8. }
  9. //非递归
  10. Node* Find(AVLTree T,int x) {
  11. 	BSTree p = T;
  12. 	while (p) {
  13. 		if (x == p->data)
  14. 			return p;
  15. 		p = x > p->data ? p->Right : p->Left;
  16. 	}
  17. 	return NULL;
  18. }

插入

左旋

先抛开AVL树的插入问题，看下面左边的二叉排序树。大家本来和平共处，突然有一天 B 觉得自己的权值比 A 大，要造反，但是B要做根结点，必须也要保证调整后的树仍然是一颗二叉排序树。

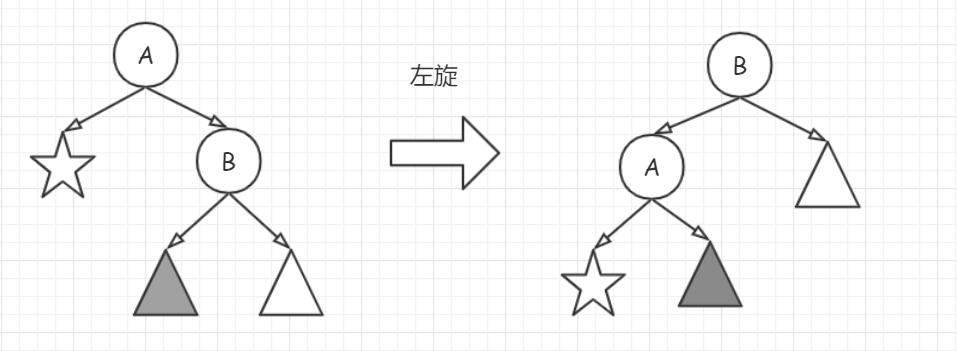
☆上所有权值都比A小， ∆ 上所有权值都比B大，无需在调整中进行位置变动；因为调整后B的左孩子变成了A，那么▲必须移动到其他地方去，因为A、B、▲的权值关系满足 A<▲<B ，所以让▲成为A的右子树即可。

这个调整过程称为左旋，分解调整过程如下：

代码如下：

  1. void L(AVLTree *root){
  2.     Node* temp = (*root)->Right; //root指向结点A，temp指向结点B
  3.     (*root)->Right = temp->Left; //图示步骤2
  4.     temp->Left = *root; //图示步骤3
  5.     root->height = max(getHeight(root->Left), getHeight(root->Rihgt)) + 1;//更新结点A高度
  6. 	temp = max(getHeight(temp->Left), getHeight(temp->Rihgt)) + 1;//更新结点B高度
  7.     *root = temp;//图示步骤4
  8. }

右旋

右旋是左旋的逆过程，如下：

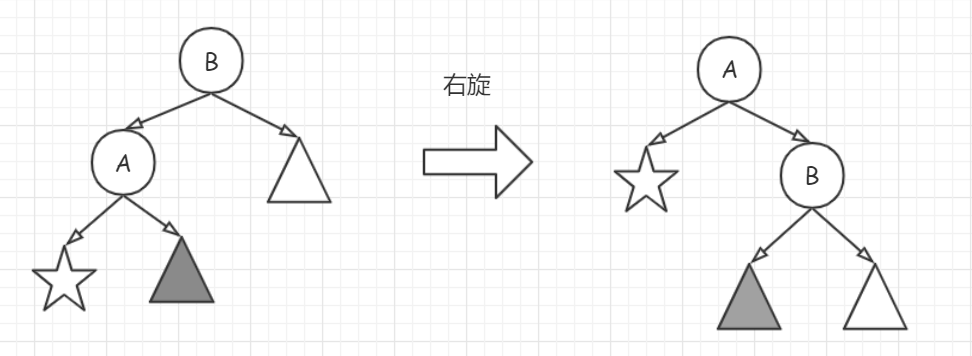
分解调整过程如下：

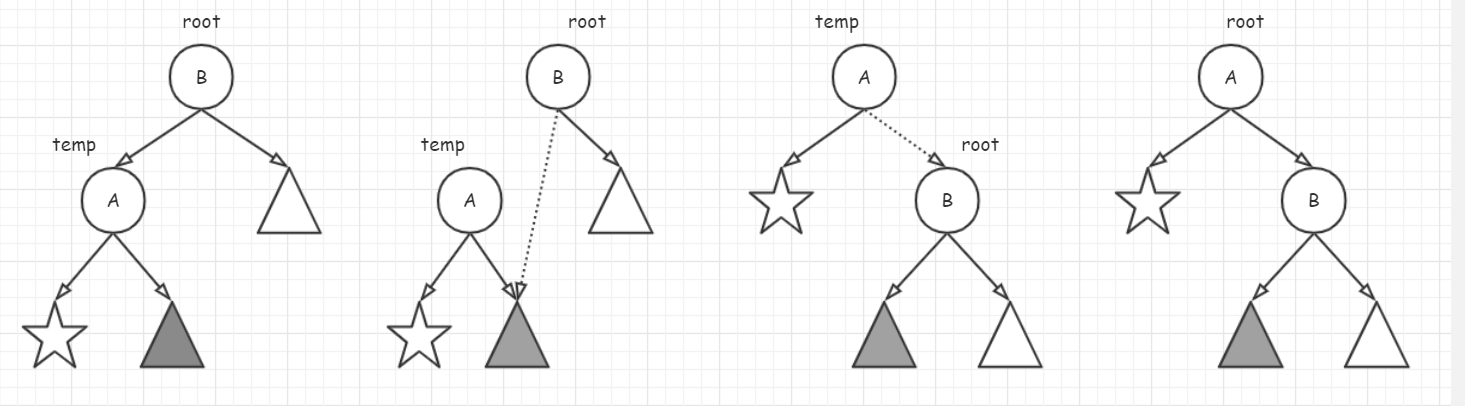
代码如下：

  1. void R(AVLTree *root) {
  2.     Node* temp = (*root)->Left;//root指向结点B，temp指向结点A
  3.     (*root)->Left = temp->Right;
  4.     temp->Right = *root;
  5.     root->height = max(getHeight(root->Left), getHeight(root->Rihgt)) + 1;
  6. 	temp = max(getHeight(temp->Left), getHeight(temp->Rihgt)) + 1;
  7.     *root = temp;
  8. }

​ 接下来讨论AVL树的插入操作，假设现在已经有一颗平衡二叉树，那么在向其中插入一个结点时，一定会有结点的平衡因子发生改变，此时就可能会有结点的平衡因子大于1 ，这样以该结点为根结点的子树就是失去平衡的，会使平衡二叉树发生失衡的情况可以分为下面四种：

LL、RR型

左左（LL）、右右（RR），LL，RR只表示树型（导致树失去平衡的插入位置），不是左旋、右旋的意思。

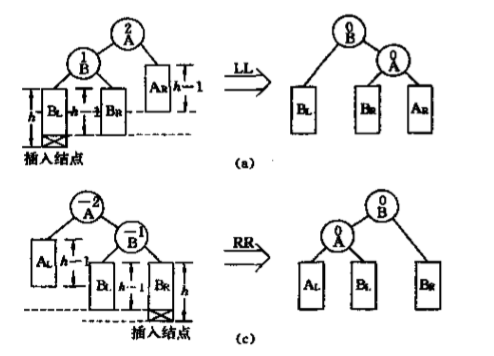
对于LL型，需要以A结点为根进行右旋；

对于RR型，需要以A为根结点进行左旋。

所以代码如下：

  1. void RR_Rotate(AVLTree *root){
  2.   	L(root);
  3. }
  5. void LL_Rotate(AVLTree *root) {
  6.     R(root);
  7. }

LR，RL型

左右（LR）、右左（RL）。

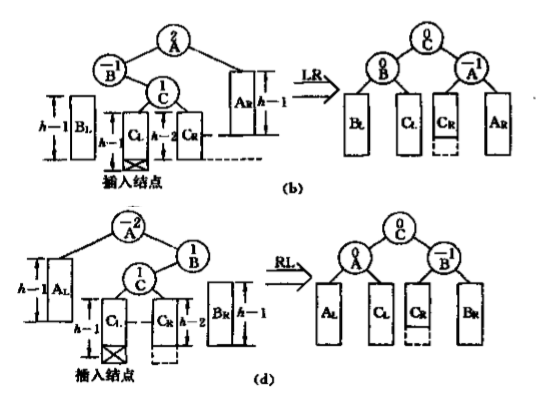
对于LR型，需要先以B结点为根结点进行一次左旋，再以A结点为根结点进行一次右旋。

对于RL型，需要先以B结点为根结点进行一次右旋，再以A结点为根结点进行一次左旋。

  1. void LR_Rotate(AVLTree *root) {
  2.     L(&(*root)->Left);
  3.     R(root);
  4. }
  5. void RL_Rotate(AVLTree *root) {
  6.     R(&(*root)->Right);
  7.     L(root);
  8. }

插入结点

插入算法就是出现不平衡状态时，判断需要使用哪种旋转方式来使得二叉树保持平衡

  1. AVLTree InsertAVLTree(AVLTree root, int x) {
  2.     if (root == NULL) {
  3.         root = new Node;
  4.         root->Left = NULL;
  5.         root->Right = NULL;
  6.         root->data = x;
  7.         return root;
  8.     }
  9.     if (x > root->data) {
  10.         	//递归返回插入位置的父节点或者祖父……。
  11.             root->Right = InsertAVLTree(root->Right, x);
  12.             //如果插入之后失去了平衡
  13.             if (height(root->Left) - height(root->Right) == -2) {
  14.                 //如果插入的值大于,当前节点的左孩子节点，说明该节点是插在root的右子树上的
  15.                 if (x > root->Left->data) RR_Rotate(&root);
  16.                 else RL_Rotate(&root);
  17.             }
  18.     }
  20.     else if (x < root->data) {
  21.         root->Left = InsertAVLTree(root->Left, x);
  22.         if (height(root->Left) - height(root->Right) == 2) {
  23.             if (x < root->Left->data) LL_Rotate(&root);
  24.             else LR_Rotate(&root);
  25.         }
  26.     }
  27.     else {
  28.         cout << "the number is already included." << endl;
  29.         return NULL;
  30.     }
  31.     return root;
  32. }

删除结点

和二叉排序树的节点的删除差不多，就是多出来一个判断从哪个子树删除节点的问题。

  1. void AVLTreeDel(AVLTree *root, int data)
  2. {
  3.     if (!*root) {
  4.         cout << "delete failed" << endl;
  5.         return;
  6.     }
  7.     Node *p = *root;
  8.     if (data == p->data) {
  9.         //左右子树都非空
  10.         if (p->Left && p->Right) {
  11.             //在高度更大的那个子树上进行删除操作
  12.             //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
  13.             if (height(p->Left) > height(p->Right)) {
  14.                 Node *pre=NULL,*q = p->Left;
  15.                 if (!q->Right)
  16.                     q->Right = p->Right;
  17.                 else {
  18.                     while (q->Right) {
  19.                         pre = q;
  20.                         q = q->Right;
  21.                     }
  22.                     pre->Right = q->Left;
  23.                     q->Left = p->Left;
  24.                     q->Right = p->Right;
  25.                 }
  26.                 *root = q;
  27.             }
  28.             else {
  29.                 Node *pre = NULL, *q = p->Right;
  30.                 if (!q->Left)
  31.                     q->Left = p->Left;
  32.                 else {
  33.                     while (q->Left) {
  34.                         pre = q;
  35.                         q = q->Left;
  36.                     }
  37.                     pre->Left = q->Right;
  38.                     q->Left = p->Left;
  39.                     q->Right = p->Right;
  40.                 }
  41.                 *root=q;
  42.             }
  43.         }
  44.         else
  45.             (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
  46.         delete p;
  47.     }
  48.     else if (data < p->data){//要删除的节点在左子树中
  49.         //在左子树中进行递归删除
  50.         AVLTreeDel(&(*root)->Left, data);
  51.         //判断是否仍然满足平衡条件
  52.         if (height(p->Right) - height(p->Left) == 2){
  53.             //如果当前节点右孩子的左子树更高
  54.             if (height(p->Right->Left) > height(p->Right->Right))
  55.                 RL_Rotate(root);
  56.             else
  57.                 RR_Rotate(root);
  58.         }
  59.     }
  60.     else{
  61.         AVLTreeDel(&(*root)->Right, data);
  62.         if (height(p->Left) - height(p->Right) == 2) {
  63.             if (height((*root)->Left->Left) > height((*root)->Left->Right))
  64.                 LL_Rotate(root);
  65.             else
  66.                 LR_Rotate(root);
  67.         }
  68.     }
  69. }

完整测试代码：

  1. #pragma once
  2. #include "top.h"
  4. typedef BTreeNode Node, *AVLTree;
  6. void RR_Rotate(AVLTree *root){
  7.     Node* Right = (*root)->Right;
  8.     (*root)->Right = Right->Left;
  9.     Right->Left = *root;
  10.     *root = Right;
  11. }
  13. void LL_Rotate(AVLTree *root) {
  14.     Node* Left = (*root)->Left;
  15.     (*root)->Left = Left->Right;
  16.     Left->Right = *root;
  17.     *root = Left;
  18. }
  19. void LR_Rotate(AVLTree *root) {
  20.     RR_Rotate(&(*root)->Left);
  21.     return LL_Rotate(root);
  22. }
  23. void RL_Rotate(AVLTree *root) {
  24.     LL_Rotate(&(*root)->Right);
  25.     RR_Rotate(root);
  26. }
  27. AVLTree AVLTreeInsert(AVLTree root, int x) {
  28.     if (root == NULL) {
  29.         root = new Node;
  30.         root->Left = NULL;
  31.         root->Right = NULL;
  32.         root->data = x;
  33.         return root;
  34.     }
  35.     if (x > root->data) {
  36.             root->Right = AVLTreeInsert(root->Right, x);
  37.             //递归返回插入位置的父节点或者祖父……，如果失去了平衡
  38.             if (height(root->Left) - height(root->Right) == -2) {
  39.             //如果插入的值大于,当前节点的右孩子节点，说明该节点是插在root的右子树上的
  40.                 //if (x > root->Left->data) RR_Rotate(&root);不能保证该节点一定有左子树
  41.                 if (x > root->Right->data)RR_Rotate(&root);
  42.                 else RL_Rotate(&root);
  43.             }
  44.     }
  45.     else if (x < root->data) {
  46.         root->Left = AVLTreeInsert(root->Left, x);
  47.         if (height(root->Left) - height(root->Right) == 2) {
  48.             if (x < root->Left->data) LL_Rotate(&root);
  49.             else LR_Rotate(&root);
  50.         }
  51.     }
  52.     else {
  53.         cout << "the number is already included." << endl;
  54.         return NULL;
  55.     }
  56.     return root;
  57. }
  59. AVLTree AVLTreeCreat(int *a, int length) {
  60.     AVLTree T = NULL;
  61.     for (int i = 0; i < length; i++) {
  62.         T = AVLTreeInsert(T, a[i]);
  63.     }
  64.     return T;
  65. }
  66. Node* AVLFind(AVLTree T, int x) {
  67.     Node *p = T;
  68.     while (p) {
  69.         if (x == p->data) break;
  70.         p = x > p->data ? p->Right : p->Left;
  71.     }
  72.     return p;
  73. }
  75. AVLTree AVLMax(AVLTree p)
  76. {
  77.     if (!p) return NULL;
  78.     if (p->Right == NULL)
  79.         return p;
  80.     return AVLMax(p->Right);
  81. }
  83. AVLTree AVLMin(AVLTree p)
  84. {
  85.     if (!p)
  86.         return NULL;
  87.     if (p->Left == NULL)
  88.         return p;
  89.     return AVLMin(p->Left);
  90. }
  92. void AVLTreeDel(AVLTree *root, int data)
  93. {
  94.     if (!*root) {
  95.         cout << "delete failed" << endl;
  96.         return;
  97.     }
  98.     Node *p = *root;
  99.     if (data == p->data) {
  100.         //左右子树都非空
  101.         if (p->Left && p->Right) {
  102.             //在高度更大的那个子树上进行删除操作
  103.             //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
  104.             if (height(p->Left) > height(p->Right)) {
  105.                 Node *pre=NULL,*q = p->Left;
  106.                 if (!q->Right)
  107.                     q->Right = p->Right;
  108.                 else {
  109.                     while (q->Right) {
  110.                         pre = q;
  111.                         q = q->Right;
  112.                     }
  113.                     pre->Right = q->Left;
  114.                     q->Left = p->Left;
  115.                     q->Right = p->Right;
  116.                 }
  117.                 *root = q;
  118.             }
  119.             else {
  120.                 Node *pre = NULL, *q = p->Right;
  121.                 if (!q->Left)
  122.                     q->Left = p->Left;
  123.                 else {
  124.                     while (q->Left) {
  125.                         pre = q;
  126.                         q = q->Left;
  127.                     }
  128.                     pre->Left = q->Right;
  129.                     q->Left = p->Left;
  130.                     q->Right = p->Right;
  131.                 }
  132.                 *root=q;
  133.             }
  134.         }
  135.         else
  136.             (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
  137.         delete p;
  138.     }
  139.     else if (data < p->data){//要删除的节点在左子树中
  140.         //在左子树中进行递归删除
  141.         AVLTreeDel(&(*root)->Left, data);
  142.         //判断是否仍然满足平衡条件
  143.         if (height(p->Right) - height(p->Left) == 2){
  144.             //如果当前节点右孩子的左子树更高
  145.             if (height(p->Right->Left) > height(p->Right->Right))
  146.                 RL_Rotate(root);
  147.             else
  148.                 RR_Rotate(root);
  149.         }
  150.     }
  151.     else{
  152.         AVLTreeDel(&(*root)->Right, data);
  153.         if (height(p->Left) - height(p->Right) == 2) {
  154.             if (height((*root)->Left->Left) > height((*root)->Left->Right))
  155.                 LL_Rotate(root);
  156.             else
  157.                 LR_Rotate(root);
  158.         }
  159.     }
  160. }
  162. int height(BTree L) {
  163. 	if (L == NULL)
  164. 		return 0;
  165. 	int left = height(L->Left);
  166. 	int right = height(L->Right);
  167. 	return left >= right ? left + 1 : right + 1;
  168. }
  170. void checkCreat() {
  171.     int length = 10;
  172.     int *a = getNoRepateRandomArray(length, 10);
  174.     for (int i = 0; i < length; i++) {
  175.         cout << a[i] << ",";
  176.     }
  178.     cout << endl;
  179.     AVLTree T = AVLTreeCreat(a, length);
  180.     int t = rand() % length;
  181.     AVLTreeDel(&T, a[t]);
  182.     for (int i = t; i < length - 1; i++) {
  183.         a[i] = a[i + 1];
  184.     }
  186.     Preorder(T);
  187.     cout << endl;
  188.     Inorder(T);
  189.     cout << endl;
  190.     Postorder(T);
  191.     cout << endl;
  192.     free(a);
  193. }

数据结构篇——平衡二叉树（AVL树）的更多相关文章

  1. 二叉查找树（BST)、平衡二叉树(AVL树)（只有插入说明）

    二叉查找树(BST).平衡二叉树(AVL树)(只有插入说明) 二叉查找树(BST) 特殊的二叉树,又称为排序二叉树.二叉搜索树.二叉排序树. 二叉查找树实际上是数据域有序的二叉树,即对树上的每个结点, ...

  2. Java 树结构实际应用 四（平衡二叉树/AVL树）

    平衡二叉树(AVL 树) 1 看一个案例(说明二叉排序树可能的问题) 给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.  左边 BST 存在的问题分析: ...

  3. 平衡二叉树,AVL树之图解篇

    学习过了二叉查找树,想必大家有遇到一个问题.例如,将一个数组{1,2,3,4}依次插入树的时候,形成了图1的情况.有建立树与没建立树对于数据的增删查改已经没有了任何帮助,反而增添了维护的成本.而只有建 ...

  4. 二叉查找树（BST)、平衡二叉树(AVL树)

    二叉查找树(BST) 特殊的二叉树,又称为排序二叉树.二叉搜索树.二叉排序树. 二叉查找树实际上是数据域有序的二叉树,即对树上的每个结点,都满足其左子树上所有结点的数据域均小于或等于根结点的数据域,右 ...

  5. 图解:平衡二叉树,AVL树

    学习过了二叉查找树,想必大家有遇到一个问题.例如,将一个数组{1,2,3,4}依次插入树的时候,形成了图1的情况.有建立树与没建立树对于数据的增删查改已经没有了任何帮助,反而增添了维护的成本.而只有建 ...

  6. 【数据结构】平衡二叉树—AVL树

    (百度百科)在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下都是O(log n).增 ...

  7. 平衡二叉树,AVL树之代码篇

    看完了第一篇博客,相信大家对于平衡二叉树的插入调整以及删除调整已经有了一定的了解,下面,我们开始介绍代码部分. 首先,再次提一下使用的结构定义 typedef char KeyType; //关键字 ...

  8. 大话数据结构—平衡二叉树(AVL树)

    平衡二叉树(Self-Balancing Binary Search Tree/Height-Balanced Binary Search Tree),是一种二叉排序树,当中每个节点的左子树和右子树的 ...

  9. 平衡二叉树-AVL树(LL、RR、LR、RL旋转)

    平衡二叉树的定义: 任意的左右子树高度差的绝对值不超过1,将这样的二叉树称为平衡二叉树,二叉平衡树前提是一个二叉排序树. 平衡二叉树的插入: 二叉平衡树在插入或删除一个结点时,先检查该操作是否导致了树 ...

随机推荐

  1. POJ2718Smallest Difference(暴力全排列)

    传送门 题目大意:升序输入十进制数 没有重复 分成两个非空集合 每个集合组成一个数(不能有前导零) 求两个数差的最小值. 题解:全排列...我数组从1开始怎么一直WA...还有这个输入值得学习. 代码 ...

  2. c++基础第一篇

    前言:我是从c和c++对比的角度来讲解c++的基础知识. (1)c++格式如下: #include <iostream> //标准输入输出头文件 using namespace std; ...

  3. 爬虫，爬取景点信息采用pandas整理数据

    一.首先需要导入我们的库函数 导语:通过看网上直播学习得到,如有雷同纯属巧合. import requests#请求网页链接import pandas as pd#建立数据模型from bs4 imp ...

  4. [LeetCode] 74. Search a 2D Matrix 搜索一个二维矩阵

    Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the follo ...

  5. 做作业时看到的 Demo

    public class HelloWorld { public static void main(String[] args) { outer: for(int i = 0;i < 3; i+ ...

  6. Salesforce 版本控制 - VS Code + GitHub + Salesforce

    使用VS Code开发Salesforce有个很好的地方是可以联接GitHub进行代码版本控制,点击查看使用VS Code开发SalesForce 第一步:安装GIthub Desktop Githu ...

  7. App.vue 不触发 beforeRouteEnter

    因为要在 router 对应一个路由的组件才可以触发 如果没有将 App.vue 作为某个路由组件(一般不会吧) 就不会触发该导航守卫 应该是想在每次进入应用时加载一些数据 所以放在 App.vue ...

  8. [Powershell]发布基于.NET Framework的WebAPI和Job控制台程序项目

    获取要发布的定时计划任务. 禁用和停止定时计划任务. 批量强制结束Job进程. 打印定时计划任务状态. 备份项目文件夹. 发布项目文件夹. 删除部署包. 启用定时计划任务. <# .NOTES ...

  9. hystrixDashboard(服务监控)

    1.新建项目 microservicecloud-consumer-hystrix-dashboard 2.yml文件 server: port: 9001 3.在pom.xml文件增加如下内容 &l ...

  10. Java8 新特性 Optional 类

    Optional 类的简介   Optional类的是来自谷歌Guava的启发,然后就加入到Java8新特性中去了.Optional类主要就是为子决解价值亿万的错误,空指针异常.   Optional ...