CSP-J2019游记&解题报告

考前一天晚上失眠.......(其实主要不是因为考试的原因)

很幸运,我们学校就是一个考点,本场作战,应该有一点加持吧.

上午在家复习,看到一篇关于PN532模拟小米手环加密卡的文章,于是,,,,,,,,你们懂的,荒废了.

下午1点过正式出征,在熟悉的学校排了一会,碰到几个同学,甚至还有小学同学!

2点半开考,先让我们看了10分钟卷子,我说这个完善程序第二题怎么这么简单啊(大雾),结果最后做自闭了....

选择题出奇简单,事实证明我全对.而且,一个基础知识题都没有!CCF真的是大刀阔斧的改革!

读程序没什么可说的,逼疯众考生第二题只试了几组数据就写出来了,错了一个判断.

就是这道:

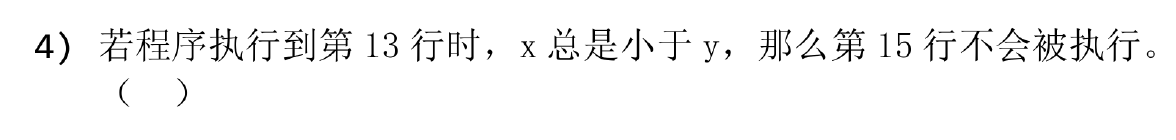
看样子是数据试少了(雾*2)

实际上你看看这答案解析不是在试数据是在干嘛!要不然谁搞得懂CCF出的鬼题是什么意思!

阅读程序第三道的最后一题,简直跪了,考场上猜了D

实际上我的思路是对的.最好的情况,也就是输出最小,就是每次都2分.

100 个节点的每层节点数量就是 （1,2,4,8,16,32,37）分别乘对应权值即可 1+4+12+32+80+192+259

但是,我天真的列出来1,2,4,8,16,32,64,算出来600多,呵呵...

完善程序第一道,简单,全对.

但这个思路清奇,加上位运算的使用,可以学习一下.

最后来说说完善程序第二道,难哭

重了几层数组,出题人不数数的吗!!!!!

好了,来说说正解.

我们先抛开双关键字,看看单关键字,最普通的基数排序.

找到一篇很好的文章:https://www.itcodemonkey.com/article/11750.html

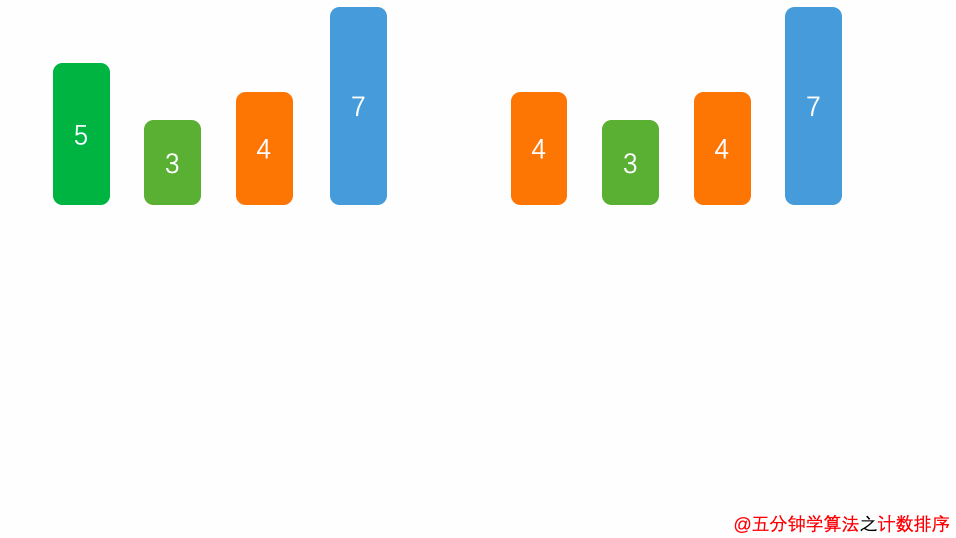
这里是计数排序算法演示

:

还有网上找的代码:

#include <iostream>
#include <stdio.h>
using namespace std;

void COUNTINGSORT(int *A,int *B,int len,int k){
    if(A == NULL || k <=  || len <= ){
        return;
    }
    int C[k+],i;
    //初始化
    for(i = ;i <= k;i++){
        C[i] = ;
    }
    //统计值为A[i]的个数,C[i]是等于i的元素个数
    for(i = ;i < len;i++){
        C[A[i]] ++;
    }
//标记1
    //确定值A[i]在最终输出数组B中位置,C[i]是小于等于i的元素个数
    for(i = ;i <= k;i++){
        C[i] += C[i-];
    }
    //输出到数组B中
    for(i = len-;i >= ;i--){
        //index元素A[i]在数组B中的下标
        int index = C[A[i]];
        B[index] = A[i];
        //如果有相同值元素的情况
        C[A[i]] --;
    }
    //B下标从1开始
}

int main(){
    int A[] = {,,,,,,,};
    int B[];
    COUNTINGSORT(A,B,,);
    for(int i = ;i <= ;i++){
        printf("%d\n",B[i]);
    }
    return ;
}

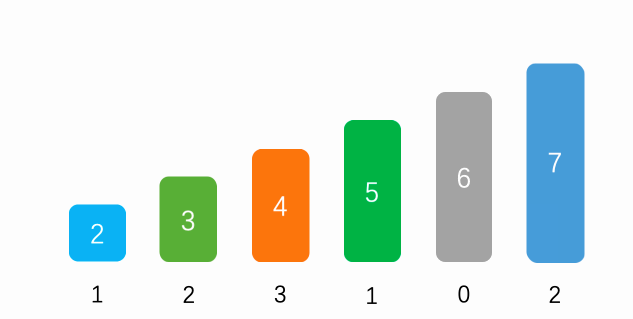
在这个地方，其实相当于把程序的标记1做完了，下面的for循环就是在做前缀和,做完后是:

1 3 6 7 7 9

做了前缀和有什么用呢?看下面代码:

for(i = len-1;i >= 0;i--){
        //index元素A[i]在数组B中的下标
        int index = C[A[i]];
        B[index] = A[i];
        //如果有相同值元素的情况
        C[A[i]] --;
    }

相当于题中的 ord[--cnt[b[i]]] = i

到这里便不难理解了.

最后回到考题双关键字,就是多套了几个数组,没什么区别.

自测分数84，等着出成绩吧，反正四川慢的很。（心里还有一点小激动呢）

最后 复赛good luck!

附2019CSP-J初赛试题及答案

链接: https://pan.baidu.com/s/1FmJHHaYZZSwDC_6J7I8x4A&shfl=shareset 提取码: u6kv