hdu4428(Coder)线段树

Coder

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2547    Accepted Submission(s): 1013

Problem Description

　
　In mathematics and computer science, an algorithm describes a set of
procedures or instructions that define a procedure. The term has become
increasing popular since the advent of cheap and reliable computers.
Many companies now employ a single coder to write an algorithm that will
replace many other employees. An added benefit to the employer is that
the coder will also become redundant once their work is done. ¹
　
　You are now the signle coder, and have been assigned a new task writing
code, since your boss would like to replace many other employees (and
you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
　
　By saying “digest sum” we study some properties of data. For the sake
of simplicity, our data is a set of integers. Your code should give
response to following operations:
　　1. add x – add the element x to the set;
　　2. del x – remove the element x from the set;
　　3. sum – find the digest sum of the set. The digest sum should be understood by

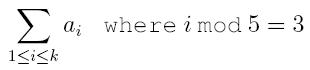
　　where the set S is written as {a₁, a₂, ... , a_k} satisfying a₁ < a₂ < a₃ < ... < a_k
　　Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
¹ See http://uncyclopedia.wikia.com/wiki/Algorithm

 

Input

　　There’re several test cases.
　　In each test case, the first line contains one integer N ( 1 <= N <= 10⁵ ), the number of operations to process.
　　Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
　　You may assume that 1 <= x <= 10⁹.
　　Please see the sample for detailed format.
　　For any “add x” it is guaranteed that x is not currently in the set just before this operation.
　　For any “del x” it is guaranteed that x must currently be in the set just before this operation.
　　Please process until EOF (End Of File).

 

Output

　
　For each operation “sum” please print one line containing exactly one
integer denoting the digest sum of the current set. Print 0 if the set
is empty.

 

Sample Input

9
add 1
add 2
add 3
add 4
add 5
sum
add 6
del 3
sum
6
add 1
add 3
add 5
add 7
add 9
sum

 

Sample Output

3
4
5

线段树：

区间一个维护该集合的个数，一个维护模5之后该集合对应1,2,3,4,0即sum[0,1,2,3,4](一一对应记录)的和。当添加一个数时，对应区间更新之后再向上更新。更新父区间时，等于左区间的Lsum[0,1,2,3,4]+右区间的Rsum[0,1,2,3,4]加上左区间个数来说。比如左区间有num个数，假设num%5 = 3,则sum[0] = Lsum[0] + Rsum[2]因为右区间的第三个数相当于整个左右区间模5余1。

sum[1] = Lsum[1] + Rsum[3],

sum[2] = Lsum[2] + Rsum[4],

sum[3] = Lsum[3] + Rsum[0],

sum[4] = Lsum[4] + Rsum[1];

即：sum[i] = Lsum[i] + Rsum[(((i - (num%5)) % 5 + 5) % 5]

 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #include <iomanip>
 #include <set>
 #include <map>
 #include <vector>
 #include <queue>
 #define N 100005
 #define llt long long int
 using namespace std;

 int num[N << ];//记录区间的个数
 llt segtree[N << ][];//
 struct node
 {
     int x;
     char s[];
 }a[N];
 int b[N];
 map<int, int> mp;//使用map离散化
 void build(int l, int r, int p)
 {
     memset(segtree[p], , sizeof(segtree[p]));
     num[p] = ;
     if (l < r)
     {
         int mid = (l + r) >> , pp = p << ;
         build(l, mid, pp);
         build(mid + , r, pp + );
     }
 }
 void update(int l, int r, int p, int pos, int v)
 {
     if (pos == l && pos == r)
     {
         segtree[p][] += 1ll * v;
         num[p] = v >  ?  : ;
         return;
     }
     int mid = (l + r) >> , pp = p << ;
     if (mid >= pos)
         update(l, mid, pp, pos, v);
     else
         update(mid + , r, pp + , pos, v);
     for (int i = ; i < ; i++)
         segtree[p][i] = segtree[pp][i] + segtree[pp + ][((i - num[pp]) %  + ) % ];
     num[p] = num[pp] + num[pp + ];
 }
 int main()
 {
     int n, i, k;
     while (~scanf("%d", &n))
     {
         k = ;
         mp.clear();
         for (i = ; i <= n; i++)
         {
             scanf("%s", a[i].s);
             if (a[i].s[] == 'a')
             {
                 scanf("%d", &a[i].x);
                 b[k++] = a[i].x;
             }
             else
                 if (a[i].s[] == 'd')
                 {
                     scanf("%d", &a[i].x);
                     a[i].x = -a[i].x;
                 }
         }
         build(, k - , );
         sort(b + , b + k);
         for (i = ; i < k; i++)
             mp[b[i]] = i;//重新编号
         for (i = ; i <= n; i++)
         {
             if (a[i].s[] == 's')
                 printf("%I64d\n", segtree[][]);
             else
                 update(, k - , , mp[abs(a[i].x)], a[i].x);
         }
     }
     return ;
 }