poj 1031 多边形对点（向周围发射光线）的覆盖

Fence

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3018		Accepted: 1010

Description

There is an area bounded by a fence on some flat field. The fence has the height h and in the plane projection it has a form of a closed polygonal line (without self-intersections), which is specified by Cartesian coordinates (Xi, Yi) of its N vertices. At the point with coordinates (0, 0) a lamp stands on the field. 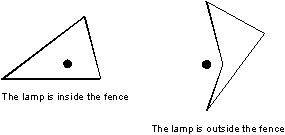The lamp may be located either outside or inside the fence, but not on its side as it is shown in the following sample pictures (parts shown in a thin line are not illuminated by the lamp): The fence is perfectly black, i.e. it is neither reflecting, nor diffusing, nor letting the light through. Research and experiments showed that the following law expresses the intensity of light falling on an arbitrary illuminated point of this fence: I₀=k/rwhere k is a known constant value not depending on the point in question, r is the distance between this point and the lamp in the plane projection. The illumination of an infinitesimal narrow vertical board with the width dl and the height h is dI=I₀*|cosα|*dl*hwhere I₀ is the intensity of light on that board of the fence, α is the angle in the plane projection between the normal to the side of the fence at this point and the direction to the lamp.  You are to write a program that will find the total illumination of the fence that is defined as the sum of illuminations of all its illuminated boards. 

Input

The first line of the input file contains the numbers k, h and N, separated by spaces. k and h are real constants. N (3 <= N <= 100) is the number of vertices of the fence. Then N lines follow, every line contains two real numbers Xi and Yi, separated by a space.

Output

Write to the output file the total illumination of the fence rounded to the second digit after the decimal point.

Sample Input

0.5 1.7 3
1.0 3.0
2.0 -1.0
-4.0 -1.0

Sample Output

5.34

题目大意：求一个用篱笆围成的多边形对灯泡发出的光单位时间吸收的能量，灯泡发出的光射到篱笆上不穿透，不反射，不衍射（即篱笆受到的光能全部吸收）。

光照强度公式：I0=k/r(I0光照强度，k固定系数，r光照点到光源的距离)

对于某一小段线段的光能量公式：dI=I0*|cosα|*dl*h（di单位时间吸收的光能，I0此处的光照强度，dl一小段篱笆的长度，h篱笆的高度，α光在这小段篱笆上的入射角的余角（设b为入射角，那么α=90-b））

设光源到这条边的距离为t:

dI=I0*|cosα|*dl*h     (cosα=t/r)

  =k/r*t/r*h*dl

  =h*k*t/(r*r)*dl

  =hkt/(t*t+l*l)*dl

l是自变量，hkt是定量，对1/(t*t+l*l)*dl积分。

根据定积分可求出这一条篱笆单位时间吸收的能量：

∫1/(t^2+l^2)dl

根据定积分公式：∫1/(a^2+x^2)dx=1/a*arctan(x/a)+c

得：∫1/(t^2+l^2)dl=1/t*arctan(l/t)+c

所以 ∫kht/(t^2+l^2)dl=kh*arctan(l/t)+c

tan(a)=l/t

接下来求原点光源发散出的光被边覆盖的总弧度和。 每条边都有它的起始极角跟终点极角,它们的角度差就为这条变覆盖光的弧度大小， 由于光不能穿透，所以有重叠的地方只能计算一遍，以x轴正方向为起始位置，光源周围的范围为（0-2*PI），每条边都有他的范围，接下来求区间覆盖就行了。 需要注意的地方：有些边穿过x正半轴这样不好处理，因此把这样的边以x正半轴切成两条边（使得每条边的起始极角都<=0，便于求区间覆盖问题）

真JB操蛋，多组案例输入就一直WA。

#include <iostream>
#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

struct Point{
    double x,y;
    Point(){}
    Point(double x,double y):x(x),y(y){}
};

struct Seg{
    double s,e;
};
typedef Point Vector;
Vector operator +(Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator -(Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator *(Vector A,double p){return Vector(A.x*p,A.y*p);}
Vector operator /(Vector A,double p){return Vector(A.x/p,A.y/p);}
bool operator < (const Point &a,const Point &b)
{
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
const double eps=1e-10;
const double PI=acos(-1*1.0);
int dcmp(double x)
{
    if(fabs(x)<eps) return 0;
    else return x<0?-1:1;
}
bool operator == (const Point &a,const Point &b){
    return (dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0);
}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}//点积
double Length(Vector A){return sqrt(Dot(A,A));}//向量长度
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}//两向量的夹角
double Cross(Vector A,Vector B){ return A.x*B.y-A.y*B.x;}//叉积
double angle(Point p){ return atan2(p.y,p.x);}
double DistanceToLine(Point P,Point A,Point B)//点到直线的距离
{
    Vector v1=B-A,v2=P-A;
    return fabs(Cross(v1,v2)) / Length(v1);
}

Point read_point()
{
    Point P;
    scanf("%lf %lf",&P.x,&P.y);
    return P;
}

vector<Point> p;
vector<Seg> s;

bool mycomp(const Seg &a,const Seg &b)
{
    if(dcmp(a.s-b.s) != 0) return a.s<b.s;
    else return a.e<b.e;
}

void swap(double &a,double &b)
{
    double t=a;
    a=b;b=t;
}

double GetAngle(Point a)
{
    double ang=angle(a);
    if(dcmp(ang) < 0) ang+=2*PI;
    return ang;
}

void SegmentDeal()
{
    int i,j,n=p.size();
    Seg s1,s2;
    for(i=0;i<n;i++)
    {
        j=(i+1)%n;
        s1.s=GetAngle(p[i]);s1.e=GetAngle(p[j]);
        if(dcmp(s1.s-s1.e) > 0) swap(s1.s,s1.e);
        if(dcmp(s1.e-s1.s-PI) > 0)
        {
            s2.s=0;s2.e=s1.s;
            s1.s=s1.e;s1.e=2*PI;
            s.push_back(s2);
        }
        s.push_back(s1);
    }
    sort(s.begin(),s.end(),mycomp);
}
double solve()
{
    int i,n;
    double L,R;
    double ans=0;
    SegmentDeal();
    n=s.size();L=s[0].s;R=s[0].e;
    for(i=1;i<n;i++)
    {
        if(dcmp(s[i].s-R) <= 0)
        {
            if(dcmp(s[i].e-R) > 0) R=s[i].e;
        }
        else
        {
            ans=R-L;
            L=s[i].s;
            R=s[i].e;
        }
    }
    ans+=R-L;
    return ans;
}

int main()
{
    int n,i;
    double h,k,ans;
    scanf("%lf %lf %d",&k,&h,&n);
    p.clear();s.clear();
    for(i=0;i<n;i++) p.push_back(read_point());
    ans=solve();
    printf("%.2lf\n",ans*h*k);
    return 0;
}