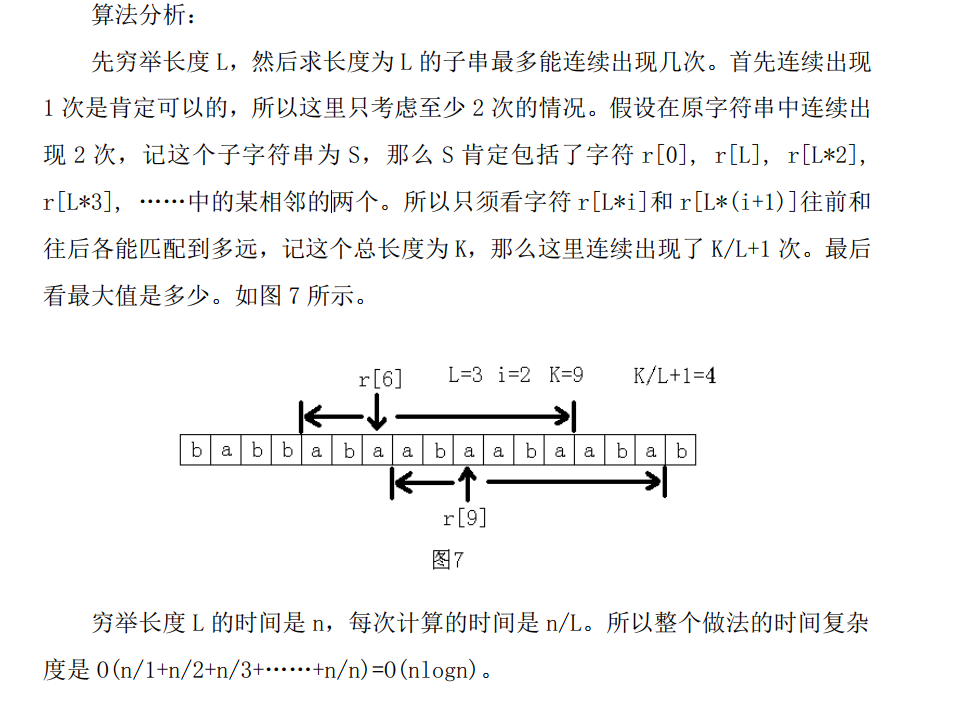
【SPOJ687&POJ3693】Maximum repetition substring（后缀数组）

题意：

n<=1e5

思路：

From http://hzwer.com/6152.html

往后匹配多远 r 用ST表求lcp即可。。。往前 l 就把串反过来再做一下。。

但是有可能求出来的最长串可以前移/后移几位
即开头可以在落在[i−l,i−l+(l+r)mod L]

区间内字典序最小的还要用ST表找rank区间最值

有空需要学习一下结构体写法 一模一样的东西写多次太累了

 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef vector<int> VI;
 #define fi first
 #define se second
 #define MP make_pair
 #define N   110000
 #define MOD 1000000007
 #define eps 1e-8
 #define pi acos(-1)
 #define oo  1000000000
 
 char ch[N];
 int n,i,s[N],sa[N],wa[N],wb[N],wc[N],wd[N],height[N],rank[N],
     ans,mx,ansl,ansr,f[][N][],g[][N],save[N],Log[N],bin[N];
 
 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }
 
 bool cmp(int *r,int a,int b,int l)
 {
     return r[a]==r[b]&&r[a+l]==r[b+l];
 }
 
 void getsa(int *r,int *sa,int n,int m)
 {
     int *x=wa,*y=wb,j,p;
     for(i=;i<n;i++) wc[x[i]=r[i]]++;
     for(i=;i<m;i++) wc[i]+=wc[i-];
     for(i=n-;i>=;i--) sa[--wc[x[i]]]=i;
     for(j=,p=;p<n;j*=,m=p)
     {
         p=;
         for(i=n-j;i<n;i++) y[p++]=i;
         for(i=;i<n;i++)
          if(sa[i]>=j) y[p++]=sa[i]-j;
         for(i=;i<n;i++) wd[i]=x[y[i]];
         for(i=;i<m;i++) wc[i]=;
         for(i=;i<n;i++) wc[wd[i]]++;
         for(i=;i<m;i++) wc[i]+=wc[i-];
         for(i=n-;i>=;i--) sa[--wc[wd[i]]]=y[i];
         swap(x,y);
         p=; x[sa[]]=;
         for(i=;i<n;i++) x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;
     }
 }    
 
 void getheight(int *r,int *sa,int n)
 {
     int i,j,k=;
     for(i=;i<=n;i++) rank[sa[i]]=i;
     for(i=;i<n;height[rank[i++]]=k)
     {
         if(k) k--;
         j=sa[rank[i]-];
         while(r[i+k]==r[j+k]) k++;
     }
 }
 
 void init()
 {
         memset(s,,sizeof(s));
         memset(sa,,sizeof(sa));
         memset(wa,,sizeof(wa));
         memset(wb,,sizeof(wb));
         memset(wc,,sizeof(wc));
         memset(wd,,sizeof(wd));
         memset(height,,sizeof(height));
         memset(rank,,sizeof(rank));
 }
 
 int lcp(int p,int x,int y)
 {
     int t;
     int L=g[p][x];
     int R=g[p][y];
     if(L>R){t=L; L=R; R=t;}
     L++;
     int q=Log[R-L+];
     return min(f[p][L][q],f[p][R-bin[q]+][q]);
 }
 
 int query(int x,int y)
 {
     int q=Log[y-x+];
     return min(f[][x][q],f[][y-bin[q]+][q]);
 }
 
 void solve(int L)
 {
     for(int i=;i+L<n;i+=L)
     if(ch[i]==ch[i+L])
     {
         int r=lcp(,i,i+L);
     //    printf("1 %d %d %d\n",i,i+L,r);
         int l=lcp(,n-i,n-i-L);
     //    printf("2 %d %d %d\n",n-i,n-i-L,l);
         if((l+r)/L+>mx) {mx=(l+r)/L+; ans=oo;}
         if((l+r)/L+==mx)
         {
             int t=query(i-l,i-l+(l+r)%L);
         //    printf("%d %d %d\n",i-l,i-l+(l+r)%L,t);
             if(t<ans)
             {
                 ans=t;
                 ansl=save[t];
                 ansr=ansl+mx*L-;
             }
         }
     }
 }
 
 int main()
 {
     //freopen("poj3693.in","r",stdin);
     //freopen("poj3693.out","w",stdout);
     bin[]=;
     for(int i=;i<;i++) bin[i]=bin[i-]<<;
     Log[]=-;
     for(int i=;i<=;i++) Log[i]=Log[i/]+;
     int cas=;
     while(scanf("%s",ch))
     {
         if(ch[]=='#') break;
         cas++;
         printf("Case %d: ",cas);
 
         init();
          n=strlen(ch);
          for(int i=;i<n;i++) s[i]=ch[i]-'a'+;
          s[n]=;
          getsa(s,sa,n+,);
          getheight(s,sa,n);
 
          for(int i=;i<n;i++) f[][i][]=rank[i];
 
          int len=Log[n];
          for(int i=;i<=n;i++) f[][i][]=height[i];
          for(int i=;i<=len;i++)
            for(int j=;j+bin[i]-<=n;j++)
             f[][j][i]=min(f[][j][i-],f[][j+bin[i-]][i-]);
         for(int i=;i<=n;i++) g[][i]=rank[i];
         for(int i=;i<=n;i++) save[i]=sa[i];
 
         init();
         for(int i=;i<n;i++) s[i]=ch[n--i]-'a'+;
          s[n]=;
          getsa(s,sa,n+,);
          getheight(s,sa,n);
 
          for(int i=;i<=n;i++) f[][i][]=height[i];
          for(int i=;i<=len;i++)
            for(int j=;j+bin[i]-<=n;j++)
            f[][j][i]=min(f[][j][i-],f[][j+bin[i-]][i-]);
         for(int i=;i<=n;i++) g[][i]=rank[i];
 
         for(int i=;i<=len;i++)
            for(int j=;j+bin[i]-<=n-;j++)
            f[][j][i]=min(f[][j][i-],f[][j+bin[i-]][i-]);
 
         ansl=ansr=;
         mx=; ans=oo;
         for(int i=;i<n;i++)
          if(ch[i]<ch[ansl]){ans=; ansl=ansr=i;}
         for(int i=;i<=n;i++) solve(i);
         for(int i=ansl;i<=ansr;i++) printf("%c",ch[i]);
         printf("\n");
     }
     return ;
 }