词典(一) 跳转表(Skip table)

词典，顾名思义，就是通过关键码来查询的结构。二叉搜索树也可以作为词典，不过各种BST，如AVL树、B-树、红黑树、伸展树，结构和操作比较复杂，而且理论上插入和删除都需要O(logn)的复杂度。

在词典中，key和value的地位相同，支持新的循值访问(call by value)的方式。因为词典的访问不再强调关键码的大小次序，因此不属于CBA式算法的范畴，因而算法的复杂度可以突破CBA算法的界限。循值访问要求在词典的内部，数据对象的数值和物理地址建立某种关联。当然，算法时间复杂度的降低，意味着空间复杂度的上升。介绍两种典型的词典，跳转表(skiptable)和哈希表(hashtable)，通过他们的操作复杂度，可以清晰地看到这一点。

词典

首先，根据词典需要的功能，定义一个词典模板类。词典需要支持的操作，主要是查询get(),插入put(),删除remove()。

 template<typename K, typename V> struct Dictionary
 {
     virtual int size() const = ;
     virtual bool put(K, V) = ;
     virtual V* get(K k) = ;
     virtual bool remove(K k) = ;
 };

跳转表

跳转表的初衷在于，相对于二叉树更加直观简便。它是一种基于链表的结构，不同之处在于，节点需要包含上下左右四个方向的指针，查询和动态操作仅需要O(logn)的时间。跳转表的总体结构如下图所示。可以看到，需要用两个链表来构成跳转表结构，其中，每一个水平链表称为一层(level)，纵向链表的规模称为层高，从S0-Sh，元素的数量递减，最底层的S0包含有表中所有的数据项；同时，同一个数据项可能在几层都出现，沿纵向组成塔(tower)，从而也需要给每一个节点定义上下两个指针。

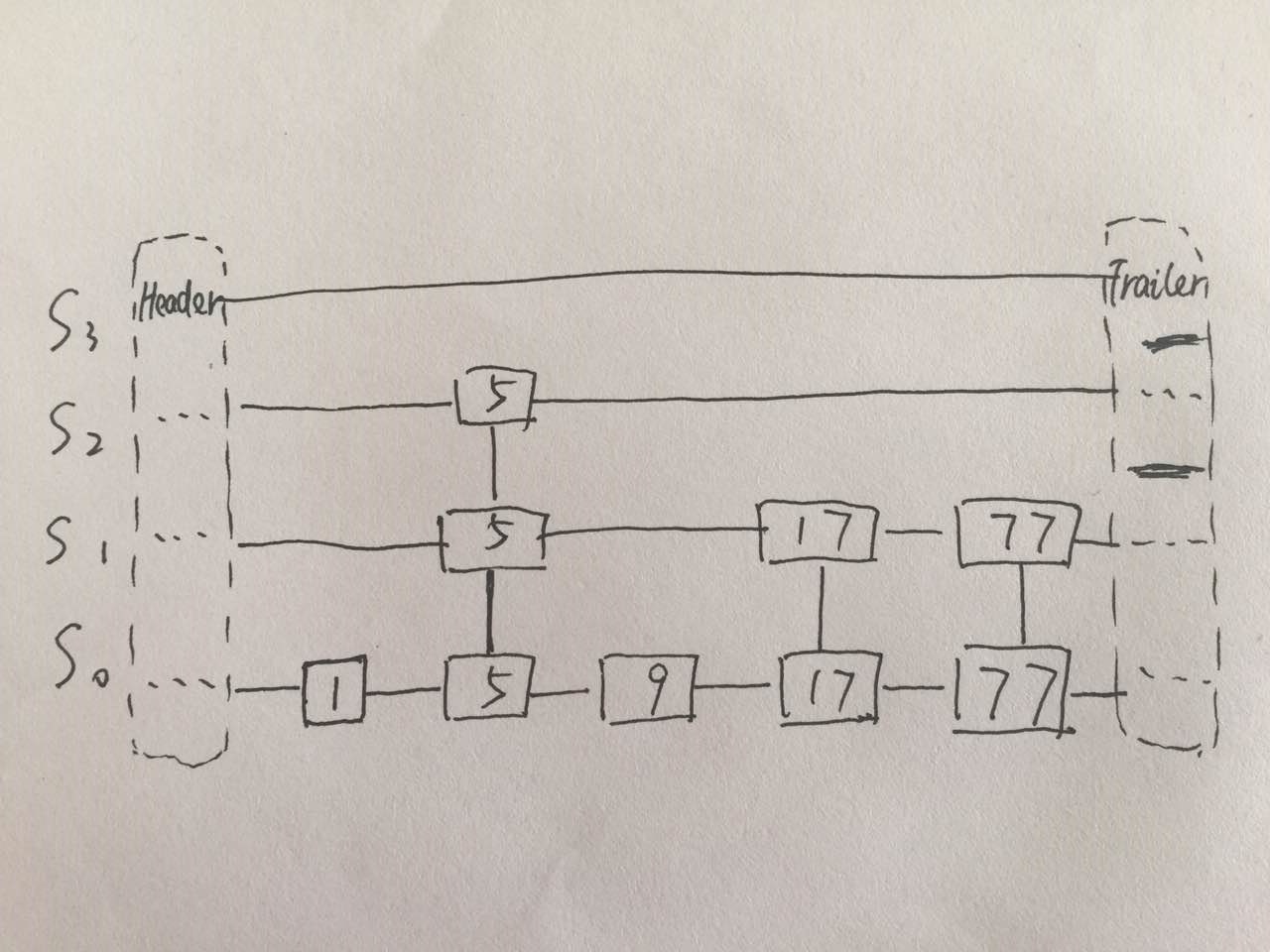
可以自然地想到，这种结构会浪费一定的空间，因为有许多不必要的重复词条，但这也正是跳转表结构效率的来源，空间换时间。如果每个词条都有很多重复，不仅接近于链表O(n)的效率，更是没有必要的浪费。因此约定，在Sk中出现的节点，也出现在Sk+1中的概率为1/2，也就是说，总体上，每一层节点只有它下一层节点数量的的一半。

为了满足四个方向都有指针的需求，需要对链表进行拓展，水平和竖直方向都可以定义后继和前驱的，称为四联表，下面是四联表的实现，总体与链表思路一致，不过因为跳转表的插入规则，只定义了after-above插入的方式。

 #include"Entry.h"
 #define QlistNodePosi(T) QuadlistNode<T>*
 template<typename T> struct QuadlistNode
 {
     T entry;
     QlistNodePosi(T) pred; QlistNodePosi(T) succ;
     QlistNodePosi(T) above; QlistNodePosi(T) below;
     QuadlistNode(T e = T(), QlistNodePosi(T) p = NULL, QlistNodePosi(T) s = NULL,
         QlistNodePosi(T) a = NULL, QlistNodePosi(T) b = NULL)
         :entry(e), pred(p), succ(s), above(a), below(b) {}
     QlistNodePosi(T) insertAsSuccAbove(T const& e, QlistNodePosi(T) b = NULL);
 };
 #include"QuadlistNode.h"
 template<typename T> class Quadlist
 {
 private:
     int _size;
     QlistNodePosi(T) header; QlistNodePosi(T) trailer;
 protected:
     void init();
     int clear();
 public:
     Quadlist() { init(); }
     ~Quadlist() { clear(); delete header; delete trailer; }
     int size() const { return _size; }
     bool empty() const{ return _size <= ; }
     QlistNodePosi(T) first() const { return header->succ; }
     QlistNodePosi(T) last() const { return trailer->pred; }
     bool valid(QlistNodePosi(T) p)
     {
         return p && (p != header) && (p != trailer);
     }
     T remove(QlistNodePosi(T) p);
     QlistNodePosi(T) insertAfterAbove(T const& e, QlistNodePosi(T) p, QlistNodePosi(T) b = NULL);
 };
 template<typename T> void Quadlist<T>::init()
 {
     header = new QuadlistNode<T>;
     trailer = new QuadlistNode<T>;
     header->succ = trailer;
     header->pred = NULL;
     trailer->pred = header;
     trailer->succ = NULL;
     header->above = trailer->above = NULL;
     header->below = trailer->below = NULL;
     _size = ;
 }
 template<typename T> T Quadlist<T>::remove(QlistNodePosi(T) p)
 {
     p->pred->succ = p->succ; p->succ->pred = p->pred;
     T e = p->entry; delete p;
     return e;
 }
 template<typename T> int Quadlist<T>::clear()
 {
     int oldsize = _size;
     while (_size > ) remove(header->succ);
     return oldsize;
 }

接下来，根据跳转表的结构，我们选取四联表作为每层的链表，所有的层数组成一个普通链表，实现跳转表的结构：

template<typename K, typename V> class Skiplist :public Dictionary<K, V>, public List<Quadlist<Entry<K, V>>*>
{
protected:
    bool skipSearch(ListNode<Quadlist<Entry<K, V>>*>* &qlist, QuadlistNode<Entry<K, V>>* &p, K& k);
public:
    int size() const { return empty() ?  : last()->data->size(); }
    int level() { return List:; size(); }
    bool put(K k, V v);//插入，允许重复故必然成功
    V* get(K k);
    bool remove(K k);
};

跳转表直接继承了链表和词典的接口，从而具备两者的功能。链表的每个节点都存储一个四联表指针，即每个节点代表了跳转表中的一层。

查找

查找接口skipSearch()，接受起始层数以及起始节点。get()可以通过调用skipSearch()来获取关键码对应的值。可以自然地想到，高层的四联表中节点少，如果能查找到，可以大大减少时间。所以，查找元素的操作，从最上层开始，如果命中，直接返回；如果未找到目标关键码，返回到不大于目标的节点，并转入下层，继续向后寻找。

 template<typename K, typename V> V* Skiplist<K,V>::get(K k)
 {
     if (empty()) return NULL;
     ListNode<Quadlist<Entry<K, V>>*>* qlist = first();
     QuadlistNode<Entry<K, V>>* p = qlist->data->first();
     return skipSearch(qlist, p, k) ? &(p->entry.value) : NULL;
 }
 template<typename K, typename V> bool Skiplist<K, V>::skipSearch(ListNode<Quadlist<Entry<K, V>>*>* &qlist,
     QuadlistNode<Entry<K, V>>* &p, K& k)
 {
     while (true)
     {
         while (p->succ && (p->entry.key <= k)) p = p->succ;
         p = p->pred;//回撤一步
         if (p->pred && (p->entry.key == k)) return true;
         qlist = qlist->succ;
         if (!qlist->succ) return false;//已经是链表的trailer,失败
         p = (p->pred) ? p->below : qlist->data->first();//转到下一层(p已经是头哨兵需要转到下一层的头哨兵)
     }
 }

因为有前面1/2概率生长的约定，空间复杂度的期望值应当为2n，总体为O(n)。相对于链表，只是增加了一个系数，但是查找时横向和纵向的复杂度，都可以大大降低。具体证明就忽略了(其实只要简单的概率论就可以了)，可以证明，跳转表的层数期望E(h)=O(logn)，整个查找过程中横向和纵向跳转次数均为O(logn)。相对于链表，牺牲了少量的空间，换区了时间复杂度的大大提升。

插入

查找操作，首先验空，若为空插入一个新的四联表。调用skipSearch()转到适当的插入位置。因为创建新节点的过程要在最底层开始，所以要转到最底层，创建一个新的塔底。剩下的任务，就是根据1/2的概率生长，如果要继续插入，那么找到上一层中的前驱节点，把新节点作为它的水平后继、以及刚插入节点的垂直后继插入。

 template<typename K, typename V> bool Skiplist<K, V>::put(K k, V v)
 {
     Entry<K, V> e = Entry<K, V>(k, v);
     if (empty()) InsertAsFirst(new Quadlist<Entry<K, V>>);//插入首个Entry（首层）
     ListNode<Quadlist<Entry<K, V>>*>* qlist = first();
     QuadlistNode<Entry<K, V>>* p = qlist->data->first();
     if (skipSearch(qlist, p, k))
         while (p->below) p = p->below;
     qlist = last();
     QuadlistNode<Entry<K, V>>* b = qlist->data->insertAfterAbove(e, p);//在最底层上插入新的基座
     while (rand() & )
     {
         while (qlist->data->valid(p) && !p->above) p = p->pred;//找到第一个比其高的前驱
         if (!qlist->data->valid(p))
         {
             if (qlist == first())//需要升层而已经是最高层时
                 InsertAsFirst(new Quadlist<Entry<K, V>>);//新加一层
             p = qlist->pred->data->first()->pred;//转至新加层的header
         }
         else
             p = p->above;
         qlist = qlist->pred;//升层
         b = qlist->data->insertAfterAbove(e, p, b);
     }
     return true;
 }

这里一定要注意一些情况，比如初始跳转表为空、寻找上一层前驱时已经为头哨兵、需要继续向上层插入而跳转表层数不足等情况。插入操作，需要进行一次查找，以及在上层寻找前驱的操作，其他的操作均为O(1)复杂度。总体上，插入操作的时间复杂度为O(logn)。

删除

删除操作相对于插入要容易一些，同样进行一次查找，从上而下顺次删除塔即可。删除完后，自上而下检查一下本层跳转表是否为空，清除空层。需要注意的是四联表的垂直方向，因为删除总是将同一个关键码的节点删除，每次删除操作后整个塔都清空，故不必再格外清除垂直方向的指针了。

 template<typename K, typename V> bool Skiplist<K, V>::remove(K k)
 {
     if (empty()) return false;
     ListNode<Quadlist<Entry<K, V>>*>* qlist = first();
     QuadlistNode<Entry<K, V>>* p = qlist->data->first();
     if (!skipSearch(qlist, p, k)) return false;
     do
     {
         QuadlistNode<Entry<K, V>>* lower = p->below;
         qlist->data->remove(p);
         p = lower; qlist = qlist->succ;//记录，向下深入删除
     } while (qlist->succ);
     while (!empty() && first()->data->empty())//如果Quadlist为空，删除
         List::remove(first());
     return true;
 }

同样，跳转表的删除操作，总体复杂度也不超过跳转表层数，即O(logn)。