HDU 4832 Chess （DP）

Chess

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 24    Accepted Submission(s): 10

Problem Description

　　小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。

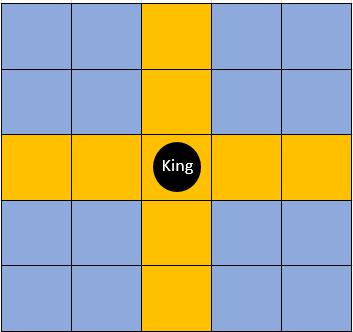
　　图1 黄色部分为棋子所控制的范围
　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x₀,y₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。
　　小良被难倒了。你能写程序解决这个问题吗？

 

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。
每组测试数据只包括一行，为五个整数N,M,K,x₀,y₀。(1≤N,M,K≤1000,1≤x₀≤N,1≤y₀≤M)

 

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

 

Sample Input

2
2 2 1 1 1
2 2 2 1 1

 

Sample Output

Case #1:
2
Case #2:
4

 

Source

2014年百度之星程序设计大赛 - 初赛（第二轮）

可以很容易发现行和列是独立的。

只要做两个一维的DP。

然后组合起来就是答案了。

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2014/5/25 14:57:15
 File Name     :E:\2014ACM\比赛\百度之星初赛2\B.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;

 const int MOD = ;
 int C[][];
 int dp1[][];
 int dp2[][];
 int x,y;
 int n,m;
 int k;
 void add(int &a,int b)
 {
     a += b;
     if(a >= MOD)a -= MOD;
 }
 int sum1[];
 int sum2[];
 void init()
 {
     C[][] = ;
     for(int i = ;i < ;i++)
     {
         C[i][] = C[i][i] = ;
         for(int j = ; j < i;j++)
         {
             C[i][j] = C[i-][j] + C[i-][j-];
             if(C[i][j] >= MOD)
                 C[i][j] -= MOD;
         }
     }
     memset(dp1,,sizeof(dp1));
     memset(dp2,,sizeof(dp2));
     dp1[y][] = ;
     for(int t = ;t <= k;t++)
         for(int i = ;i <= m;i++)
         {
             dp1[i][t] = ;
             if(i- >= )
             {
                 add(dp1[i][t],dp1[i-][t-]);
             }
             if(i -  >= )
             {
                 add(dp1[i][t],dp1[i-][t-]);
             }
             if(i +  <= m)
             {
                 add(dp1[i][t],dp1[i+][t-]);
             }
             if(i+ <= m)
             {
                 add(dp1[i][t],dp1[i+][t-]);
             }
         }
     dp2[x][] = ;
     for(int t = ;t <= k;t++)
         for(int i = ;i <= n;i++)
         {
             dp2[i][t] = ;
             if(i- >= )
             {
                 add(dp2[i][t],dp2[i-][t-]);
             }
             if(i -  >= )
             {
                 add(dp2[i][t],dp2[i-][t-]);
             }
             if(i +  <= n)
             {
                 add(dp2[i][t],dp2[i+][t-]);
             }
             if(i+ <= n)
             {
                 add(dp2[i][t],dp2[i+][t-]);
             }
         }
     memset(sum1,,sizeof(sum1));
     for(int i = ;i <= k;i++)
         for(int j = ;j <= m;j++)
             add(sum1[i],dp1[j][i]);
     memset(sum2,,sizeof(sum2));
     for(int i = ;i <= k;i++)
         for(int j = ;j <= n;j++)
             add(sum2[i],dp2[j][i]);
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int T;
     int iCase = ;
     scanf("%d",&T);
     while(T--)
     {
         iCase++;
         printf("Case #%d:\n",iCase);
         scanf("%d%d%d%d%d",&n,&m,&k,&x,&y);
         init();
         long long ans = ;
         for(int i = ;i <= k;i++)
         {
             ans += (long long)C[k][i] * sum1[i]%MOD*sum2[k-i]%MOD;
             ans %= MOD;
         }
         printf("%d\n",(int)ans);

     }
     return ;
 }