基于Python的函数回归算法验证

看机器学习看到了回归函数，看了一半看不下去了，看到能用方差进行函数回归，又手痒痒了，自己推公式写代码验证：

常见的最小二乘法是一阶函数回归
回归方法就是寻找方差的最小值
y = kx + b
xi, yi
y-yi = kxi+b-yi
方差为
∑(kxi + b - yi )^2
f = k^2∑xi^2 + b^2 + ∑yi^2 +2kb∑xi - 2k∑xi*yi - 2yib
求极值需要对其求微分，因为是二元函数，因此使用全微分公式，其极值点应该在两个元的偏微分都为0处
δf/δk = 2k∑(xi^2)+2(∑xib-∑xi*yi) = 0
δf/δb = 2b +2(k∑xi -∑yi) = 0
b = ∑yi - k∑xi
2k∑(xi^2) + 2(∑xi∑yi - k(∑xi)^2-∑xi*yi)
k = (∑xi*yi - ∑xi∑yi)/(∑(xi^2)-(∑xi)^2)
以上就是最小二乘法的推导
那么扩展到二阶函数拟合回归
y = c0+c1*x+c2*x^2
xi, yi
y - yi = c0 + c1*xi + c2*xi^2 - yi
c0^2 + c1^2∑xi^2 + c2^2∑xi^4 +yi^2...
其三元偏微分表示如下
0 = c0 + c1∑xi + c2∑xi^2 - ∑yi
0 = c1∑xi^2 + c0∑xi + c2∑xi^3 - ∑xi*yi
0 = c2∑xi^4 + c0∑xi^2 + c1∑xi^3 - ∑xi^2 * yi
解方程可以求出三个参数
更高阶的回归可就不能手解方程了，需要用线性代数的知识
y = c0 + c1 * x + c2 * x^2 + c3 * x^3

0 = c0 + c1∑xi +c2∑xi^2 + c3∑xi^3 - ∑yi
0 = c0∑xi + c1∑xi^2 + c2∑xi^3 +c3∑xi^4 - ∑xi*yi
0 = c0∑xi^2 + c1∑xi^3 + c2∑xi^4 + c3∑xi^5 - ∑xi^2*yi
0 = c0∑xi^3 + c1∑xi^4 +c2∑xi^5 +c3∑xi^6 - ∑xi^3*yi

M * [c0, c1, c2, c3]T = [∑yi, ∑xi*yi, ∑xi^2*yi, ∑xi^3*yi]T
[c0, c1, c2, c3]T = M^-1 * [∑yi, ∑xi*yi, ∑xi^2*yi, ∑xi^3*yi]T
实际上这个最终转为了求矩阵逆的过程

因此多阶函数的拟合回归本质是矩阵求逆，这对于应用数学工具而言是比较容易的

更普遍的，对于y = ∑cj*gj(x)的形式，有
Yj = ∑(i)(gj(xi) * yi)
Mj,k = ∑(i)(gj(xi) * gk(xi))
M * C = Y; C = M^(-1) * Y (M 为矩阵，C和Y为向量)
求解Ck可以得到线性参数集

数学最优美的地方就是可以化繁为简，而同样优美的是代码，使用python写出以上过程的算法验证
以下程序基于numpy和matplotlib，其实简单应用用python确实足以替代matlab了

为了防止高次计算溢出，对x, y进行归一，之前没做这步，算到四次回归就溢出了
x' = x/xmax
y' = y/ymax
y = ∑(Cj * gj(x / xmax))*ymax

对：
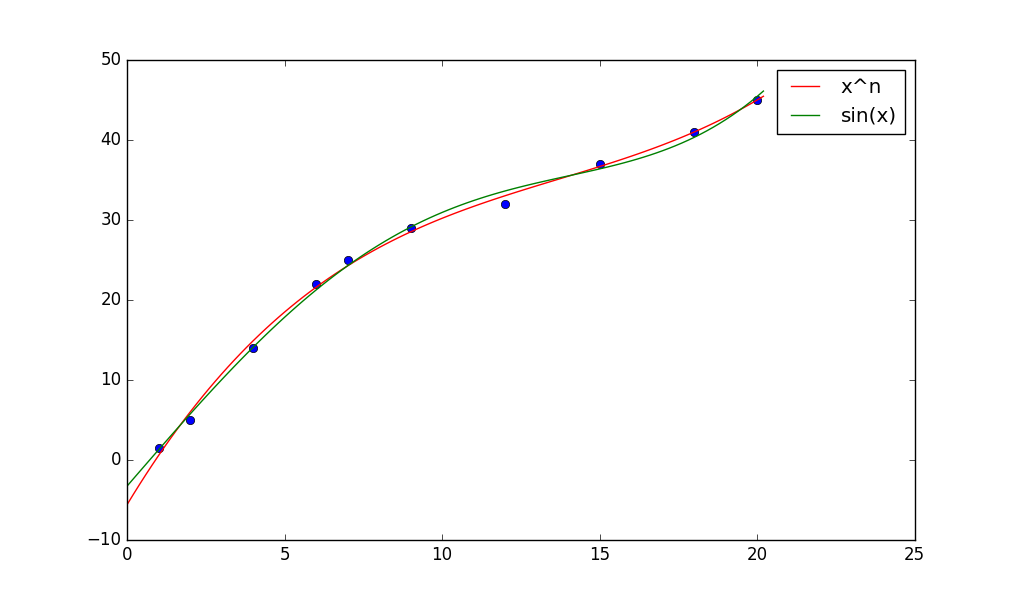
x = 1, 2, 4, 6, 7, 9, 12, 15, 18, 20
y = 1.5, 5, 14, 22, 25, 29, 32, 37, 41, 45
进行3阶函数回归计算，完整代码如下，为了强制符合PEP8规范，英文注释写的很蹩脚...
终于上代码了：

"""
name: regression
author: robocky
create time: 2017-1-1
description: Use polynomial function to fitting data
"""
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt

def polynomial(c: np.array, x: np.array, gs: list):
    """y = c0 * g0(x) + c1 * g1(x) + c2 * g2(x)...+ cn * gn(x)"""
    return c.dot(np.array([g(x) for g in gs]))

def regression(x: np.array, y: np.array, gs: list):
    """Use inv of matrix to calculate regression
    y = ∑ci * gi(x)
    """
    y_res = np.array([sum(g(x) * y) for g in gs])
    x_matrix = np.array([[sum(g(x) * h(x)) for g in gs] for h in gs])
    return inv(x_matrix).dot(y_res)

def func_gen(n):
    """Generate power functions"""
    return lambda x: x ** n

def func_gen_sin(n):
    """Generate sin functions"""
    return (lambda x: x ** 0) if n == 0 else lambda x: np.sin(n * x)

if __name__ == '__main__':
    # Test
    x_list = np.array([1, 2, 4, 6, 7, 9, 12, 15, 18, 20])
    y_list = np.array([1.5, 5, 14, 22, 25, 29, 32, 37, 41, 45])
    g_list = [func_gen(i) for i in range(4)]
    g_list2 = [func_gen_sin(i) for i in range(4)]
    # Set numbers to unit, in order to avoid overflow
    x_max, y_max = max(x_list), max(y_list)
    c_list = regression(x_list / x_max, y_list / y_max, g_list)
    c_list2 = regression(x_list / x_max, y_list / y_max, g_list2)
    # plot
    plt.figure()
    plt.plot(x_list, y_list, 'bo')
    x_line = np.arange(0, 1.02, 0.01)
    plt.plot(x_line * x_max, polynomial(c_list, x_line, g_list) * y_max, color='red', label='x^n')
    plt.plot(x_line * x_max, polynomial(c_list2, x_line, g_list2) * y_max, color='green', label='sin(x)')
    plt.legend()
    plt.show()

回归算法只有三行，当然计算过程都省略了，多项式也很简单
做了个函数生成器，理论上可以用任何函数进行回归运算，不过结果可能会发散，比如纯正弦函数，但加个常数项结果就收敛了
最后上个结果图