游走 bzoj 3143

游走

【问题描述】

【输入格式】

【输出格式】

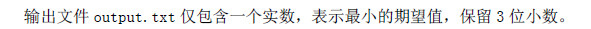
【样例输入】

3 3

2 3

1 2

1 3

【样例输出】

3.333

【样例说明】

---

题解：

题意是给一个简单无向连通图，给每条边赋上权值，使期望值最小

贪心让被走到概率大的边的权值小，就可得到最小的期望值

设每个点被走到的概率为p, 出度为d

那么p[i] = Σ p[j] / d[j] (i，j 之间有连边) (从 j 出发选到 i 与 j 连边的概率为 1 / d[j])

移项得 Σ p[j] / d[j] - p[i] = 0

对于每个点我们都可以列出一个含有n个未知数的方程

特别地，p[1]概率需要加一 , p[n] = 1 (起点为1，终点为n)

那么就可以进行高斯消元啦

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 inline void Scan(int &x)
 {
     char c;
     while((c = getchar()) < '' || c > '');
     x = c - '';
     while((c = getchar()) >= '' && c <= '') x = (x << ) + (x << ) + c - '';
 }
 double eps = 1e-;
 int n, m;
 double c[];
 double a[][];
 int x[], y[];
 int de[];
 double ans;
 inline void Solve()
 {
     int now;
     double t;
     for(int i = ; i <= n; ++i)
     {
         now = i;
         while(fabs(a[i][now]) <= eps && now <= n) ++now;
         if(now > n) continue;
         for(int j = ; j <= n + ; ++j) swap(a[i][j], a[now][j]);
         t = a[i][i];
         for(int j = ; j <= n + ; ++j) a[i][j] /= t;
         for(int j = ; j <= n; ++j)
             if(i != j)
             {
                 t = a[j][i];
                 for(int k = ; k <= n + ; ++k)
                     a[j][k] -= a[i][k] * t;
             }
     }
 }
 int main()
 {
     Scan(n), Scan(m);
     for(int i = ; i <= m; ++i)
     {
         Scan(x[i]), Scan(y[i]);
         ++de[x[i]], ++de[y[i]];
     }
     for(int i = ; i <= m; ++i)
     {
         a[x[i]][y[i]] += 1.0 / (double) de[y[i]];
         a[y[i]][x[i]] += 1.0 / (double) de[x[i]];
     }
     for(int i = ; i <= n + ; ++i) a[n][i] = ;
     for(int i = ; i <= n; ++i) a[i][i] = -;
     a[][n + ] = -;
     Solve();
     for(int i = ; i <= m; ++i)
         c[i] = a[x[i]][n + ] / (double) de[x[i]] + a[y[i]][n + ] / (double) de[y[i]];
     sort(c + , c +  + m);
     for(int i = ; i <= m; ++i)
         ans += c[i] * (m - i + );
     printf("%.3lf", ans);
 }