深入理解VUE样式style层次分析

　　刚开始使用vue的时候容易被里面的样式搞懵：

　　样式可以在main.js中引入，在模块js文件中引入，在组件中的style标签引入，在组件中的script标签引入，还可以在index.html的body中引入。

　　我不禁要问:

　　1、从不同位置引入的样式到底是什么关系？

　　2、在实际定义样式时应该定义在哪个位置，以避免样式产生的冲突？

　　纸上得来终觉浅，绝知此事要躬行。看十次文档，不如做一个测试。

　　新建一个最简单的项目并运行：如果你人品没问题，会看到弹出的浏览器中，head标签内有这样的style

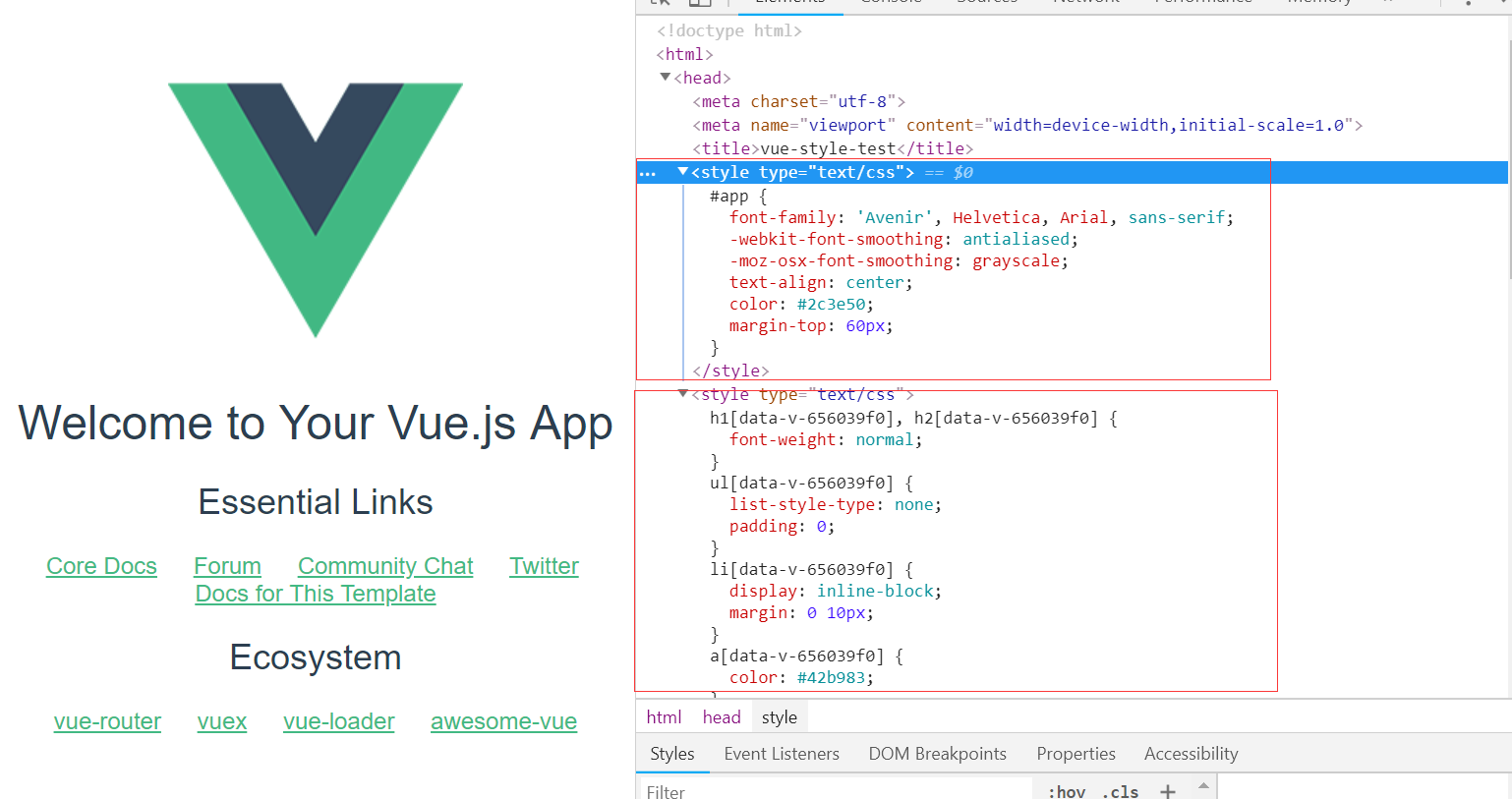
　　在项目src目录中找找看：

　　第一个style在\src\App.vue文件的style中

　　第二个style在\src\components\HelloWorld.vue文件中

　　App.vue是所有路由的出口，包含HelloWorld.vue，因此页面先加载App.vue的style，再加载HelloWorld.vue的style。看起来很简单，先加载的会先出现，根据页面样式的规则，如果有相同的类定义，后者会覆盖前者。

　　但是我想就开头出现的问题了解得更深入。为避免多个问题纠缠在一起，我逐个去分析：

加载顺序的问题

1、为方便看到测试的结果，我改造一下项目：

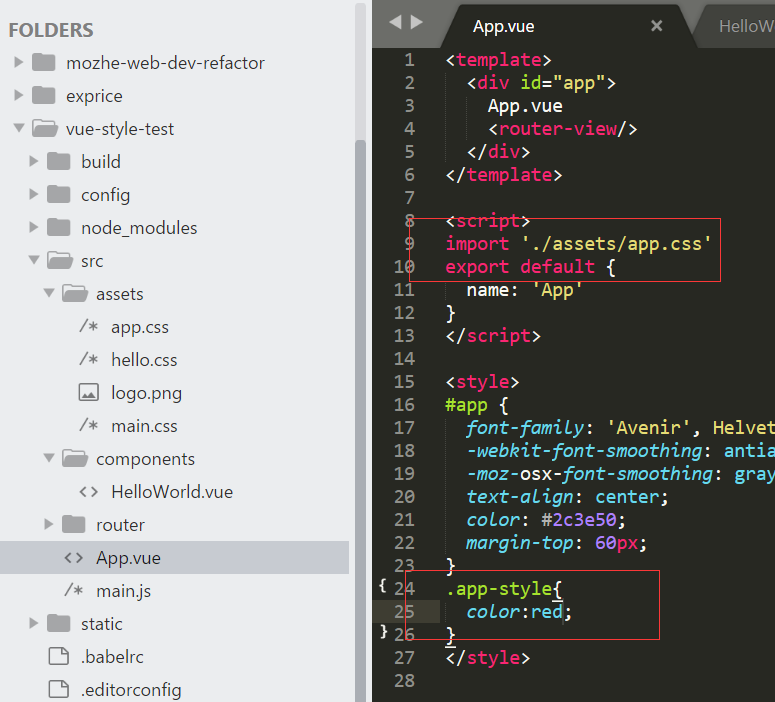
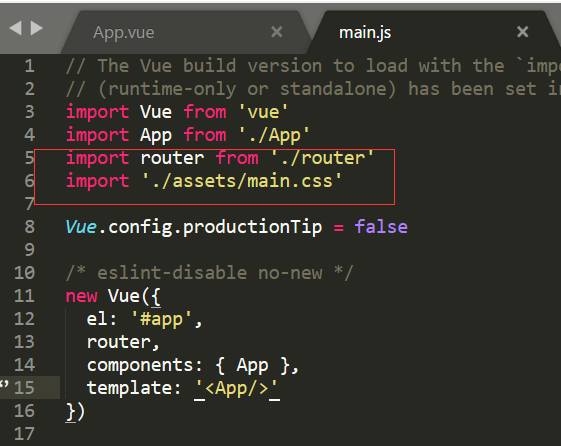
　　我只须关注main.js、App.vue、HelloWorld.vue这三个文件的样式加载，因此删除了其它无关的内容，再来看浏览器：

　　结果有点奇怪，先加载app.css，再加载hello.css，再加载main.css，

　　为什么呢？我们来看看main.js是怎么定义的：

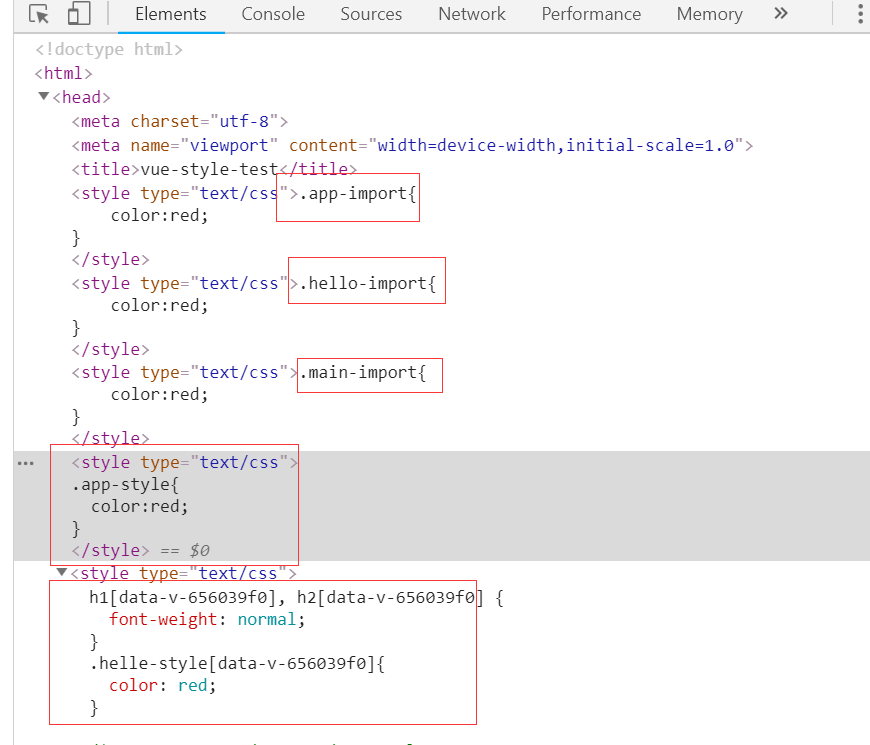
　　原来main.js里先引入了App.vue文件，所以它先执行App.vue里的script，从而引入了app.css

　　随后引入router，router里引入了HelloWorld.vue，继而加载hello.css

　　加载完App.vue后才按顺序加载main.css，于是有了上面的结果。

　　而所有组件的style都是script里的代码执行完后再加载。

　　所以我大致可以得出结论：

　　样式从main.js入口开始顺序加载，

　　遇到组件则加载组件中script所引入的样式，

　　先处理完所有scipt中的引入，

　　再处理style，

　　style按包含关系从外到内加载

　　但是问题还没完，我又得出另外的问题：这些页面都是固定的，如果是异步加载页面，当路由切换到另一个页面时，此页面原来的样式是否会删除，当前页面的样式会添加到哪里？

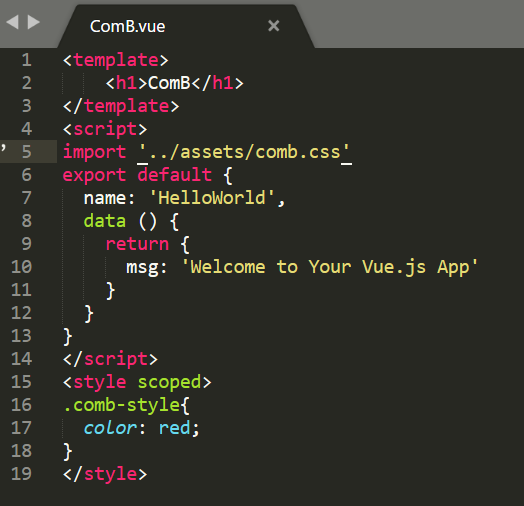
2、为此我又再路由中添加了ComB.vue，并且使用异步加载该组件。

    

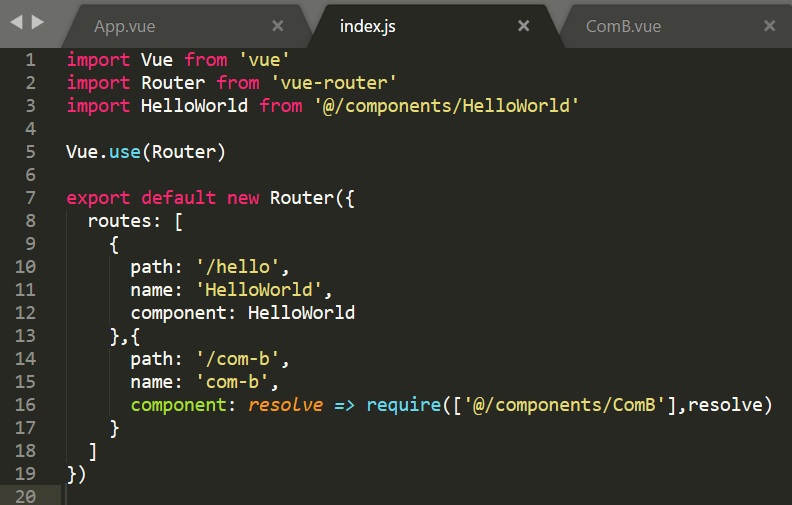
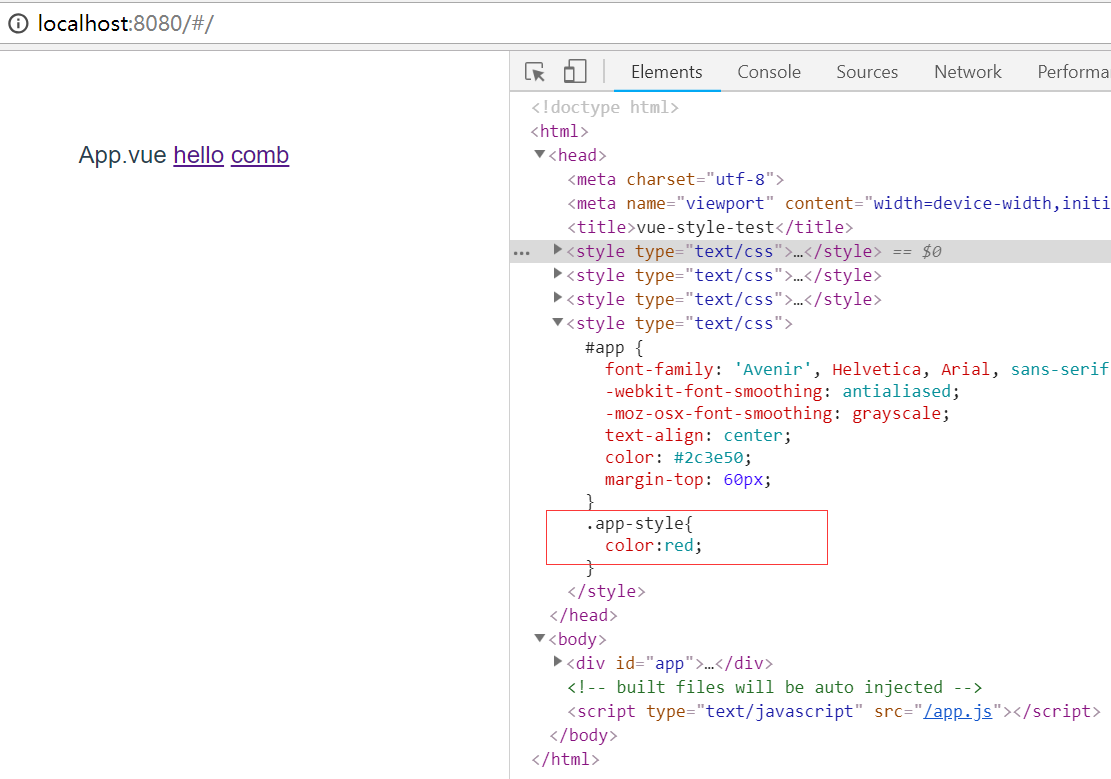
　　再看浏览器：先只会加载到app-style

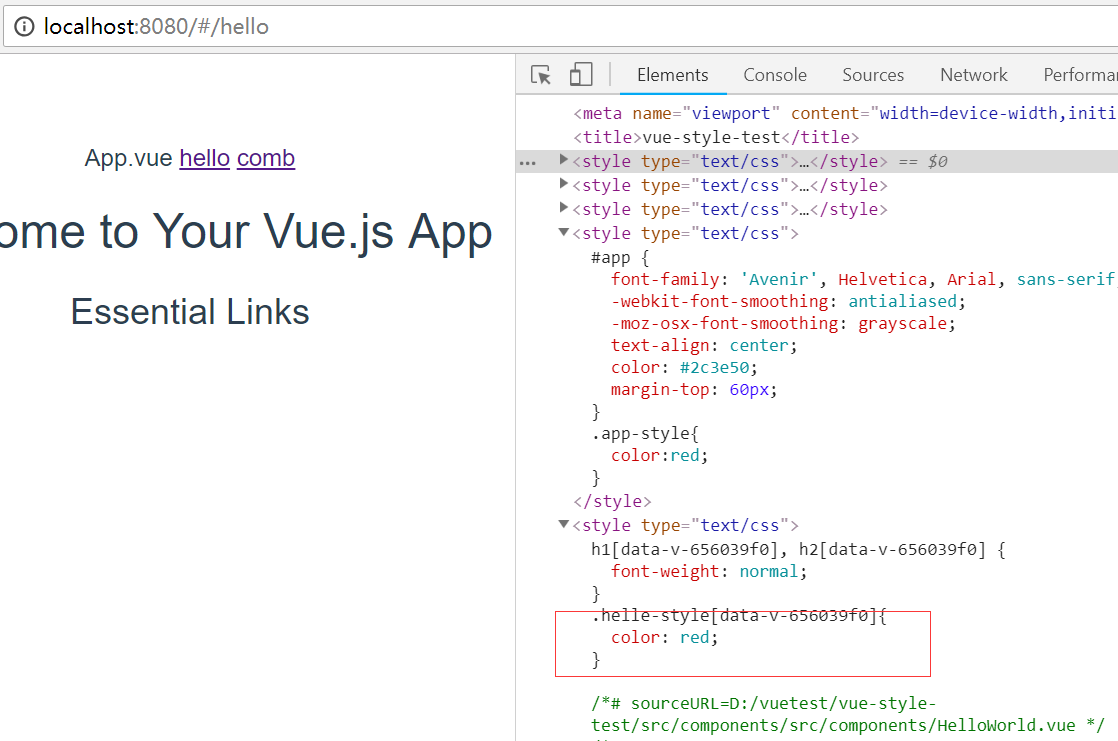
　　点击hello之后，加载hello-style

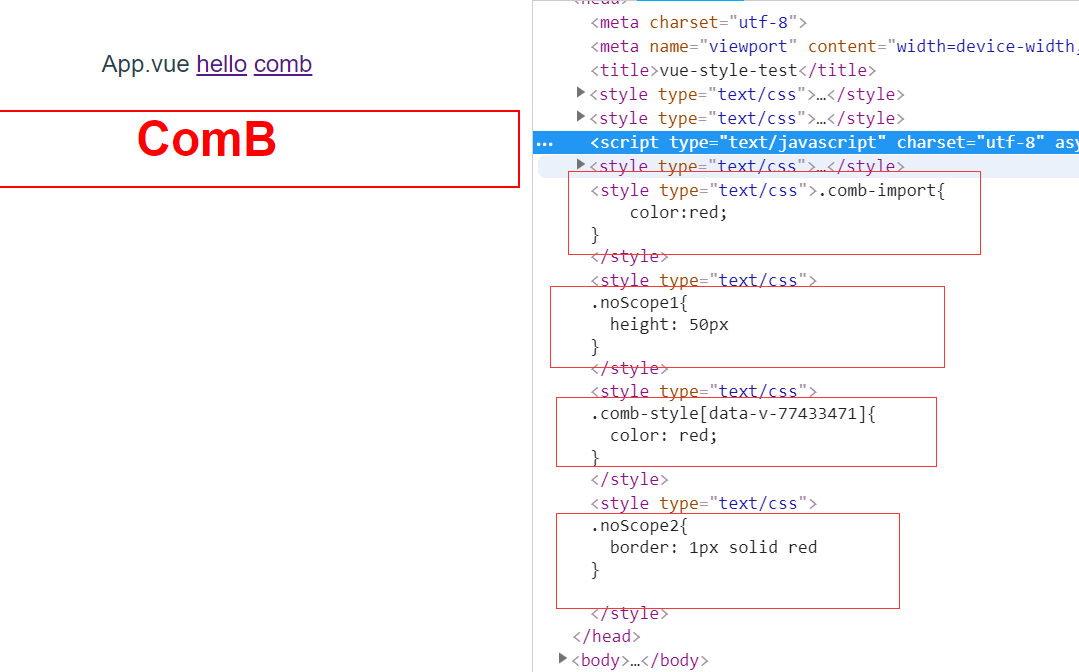
　　点击comb之后，异步加载comb组件，先引入comb-import，再引入comb-style

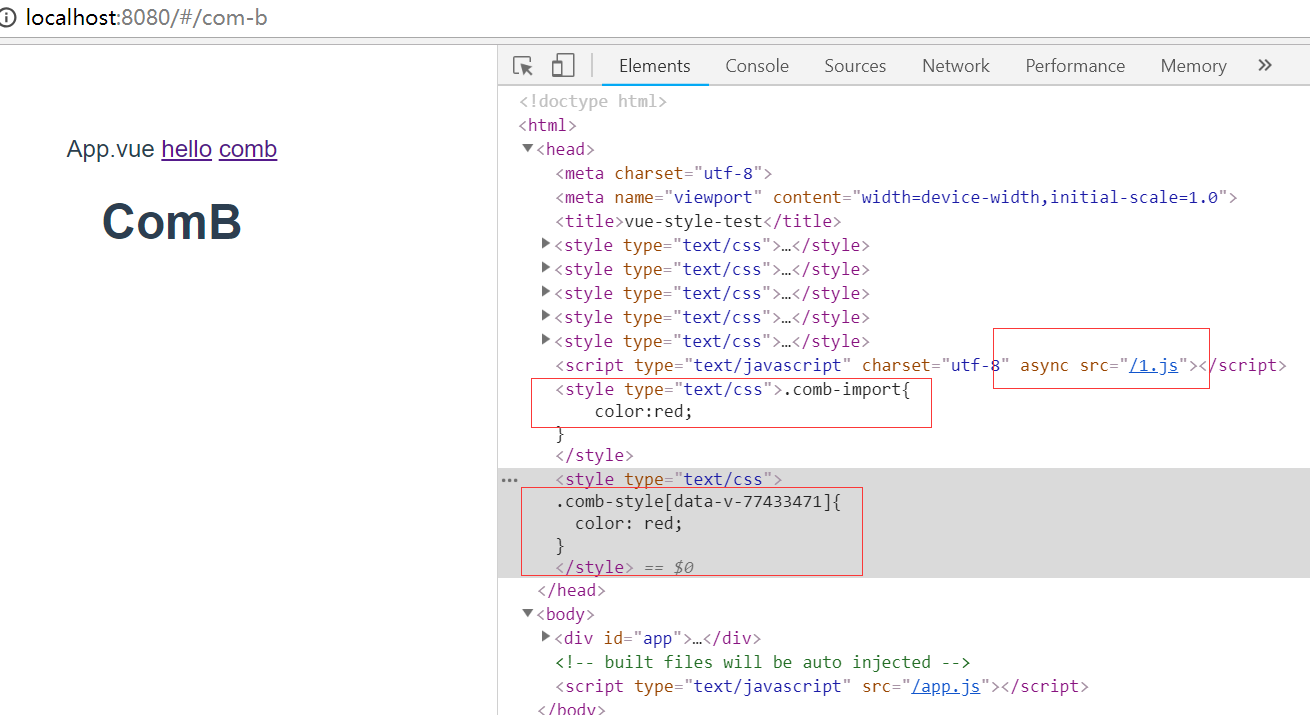
　　可以看到，浏览器先加载1.js组件文件，然后执行script加载comb.css,再加载ComB.vue的style，而当我切换回ComA页面时，head标签内的样式不再有变化。

　　另外可以看到，当我更改路由使HelloWorld不在根路径显示，HelloWorld就只加载hello.css，而不会加载HelloWorld的style，只有HelloWorld页面显示出来时才加载。

3、我再看看如果把helloworld也改成异步组件会怎么样？

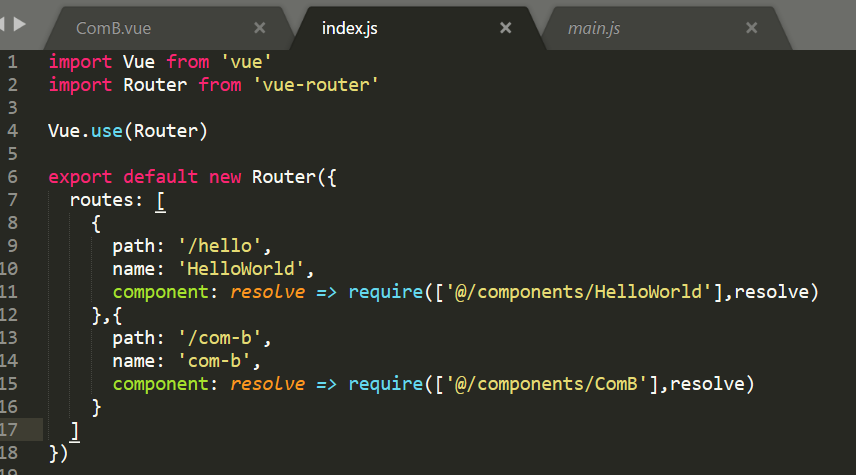
　　可以看到之前第二个加载的hello-import没有了，然后先点击谁，谁就先加载

 

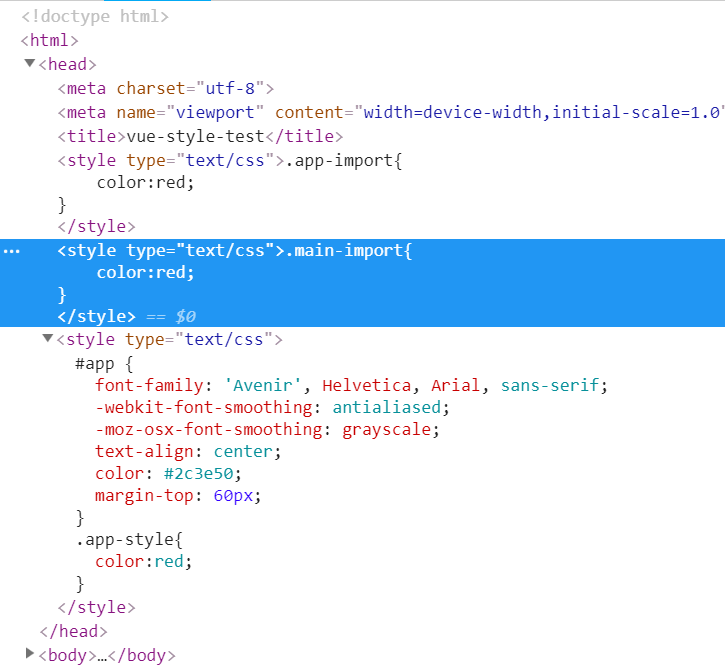
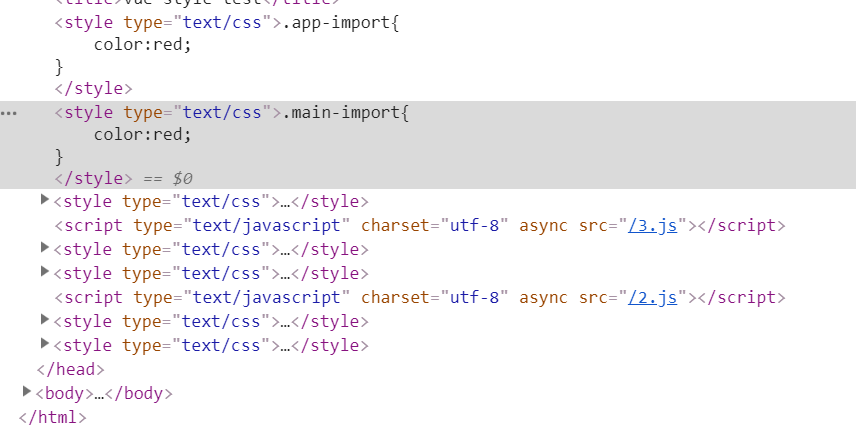
　　所以可以知道：如果ComA和ComB都是异步组件，则先打开哪一页就加载哪一页的script和style

　　再定义一个ComBB，在ComB中引入，但不显示，则ComBB只显示comb_b.css，但不显示style

　　所以：加载顺序应再加两条规则：

　　异步组件先显示的先加载

　　没有显示的页面或者组件不加载style

4、再看一个问题：一个组件内可以定义不止一个style，并且有scoped的style和没有scoped的style可以并存，它们会按照所定义的顺序加载。

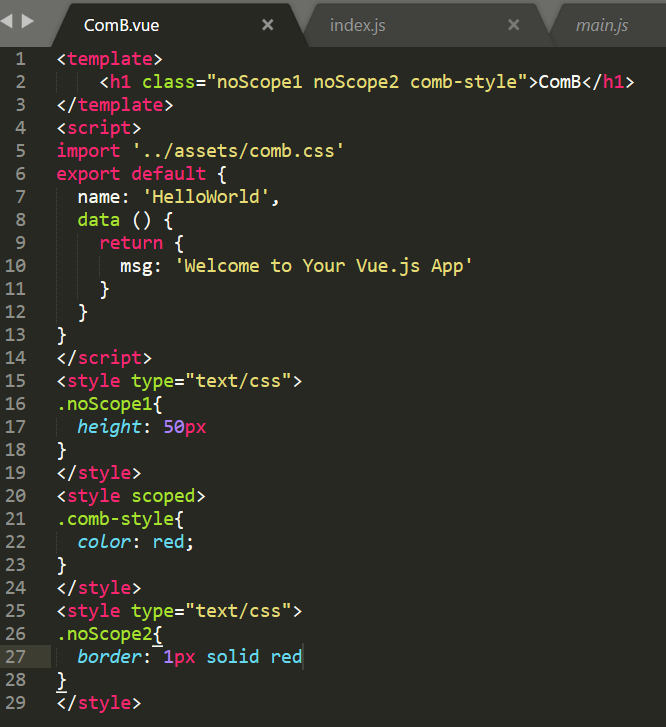
　　看浏览器，按顺序加载：

<style type="text/css">
.noScope1.noScope2{
  height: 50px
}
</style>
<style scoped>
.comb-style{
  color: red;
}
</style>
<style type="text/css">
.noScope2{
  border: 1px solid red;
  height:20px;
}
</style>

　　并且我把样式稍微做了改变，比如先给noScope2加height，发现覆盖了noScope1的高度；再然后，给.noScope1加上.noScope2，高度又变成50，

　　也就是说：跟普通CSS拥有一样的权重优先机制。

5、再看写在body内的样式

　　通过main.js控制的样式都在head标签中显示，由此就可以知道，如果我在body内定义样式，是可以把head标签内的同名样式覆盖掉的。

　　但要注意的是，在body内引入的样式，因为已经不在main.js控制范围内，也就是不参与打包，所以必须定义在static静态资源目录内。

　　同时要注意，在body引入的样式不在src文件夹内，没有热更新的功能，所以每次更改后需要手动刷新页面。

6、总结

　　经过以上的测试，可以得知style出现的顺序跟你定义的位置，是否异步组件，初始状态是否显示有关。而样式的覆盖又可以通过添加scoped和在body内添加样式文件来控制。相信单页应用要精准控制样式绝对不是难事。