Splay和LCT的复杂度分析

\(Splay\)的复杂度分析

不论插入，删除还是访问，我们可以发现它们的复杂度都和\(splay\)操作的复杂度同阶，只是一点常数的区别

我们不妨假设有\(n\)个点的\(splay\)，进行了\(m\)次\(splay\)操作

---

采用势能分析

我们记\(w(x) = \left \lceil \log_2 (size(x)) \right \rceil\)，注意以\(2\)为底和上取整

我们定义势能函数为\(\varphi = \sum w(x)\)

（记第\(i\)次操作操作完之后，势能为\(\varphi(i)\)）

只需要估计出\(\varphi(m) - \varphi(m - 1) + \varphi(m - 1) - \varphi(m - 2) ... + \varphi(1) - \varphi(0) + \varphi(0)\)的大小即可

（即初始势能和每次的势能变化量的和）

显然，\(\varphi(0) \leqslant n \log n\)

---

\(splay\)操作的具体定义为：

如果父节点是根，那么旋转一次

如果父节点和爷节点所处子树方向一致，那么先旋转父亲再旋转自己

否则，旋转两次自己

实际上可以归结于\(zig\)，\(zag\)，\(zig-zig\)，\(zag-zag\)，\(zig-zag\)，\(zag-zig\)操作

由于\(zig\)和\(zag\)是对称的操作

因此，只需要对\(zig\)，\(zig-zig\)，\(zig-zag\)操作分析复杂度即可

---

\(zig\)操作

势能的变化量为\(1 + w'(x) + w'(fa) - w(x) - w(fa) \leq 1 + w'(fa) - w(x) \leq 1 + w'(x) - w(x)\)

---

\(zig-zig\)操作

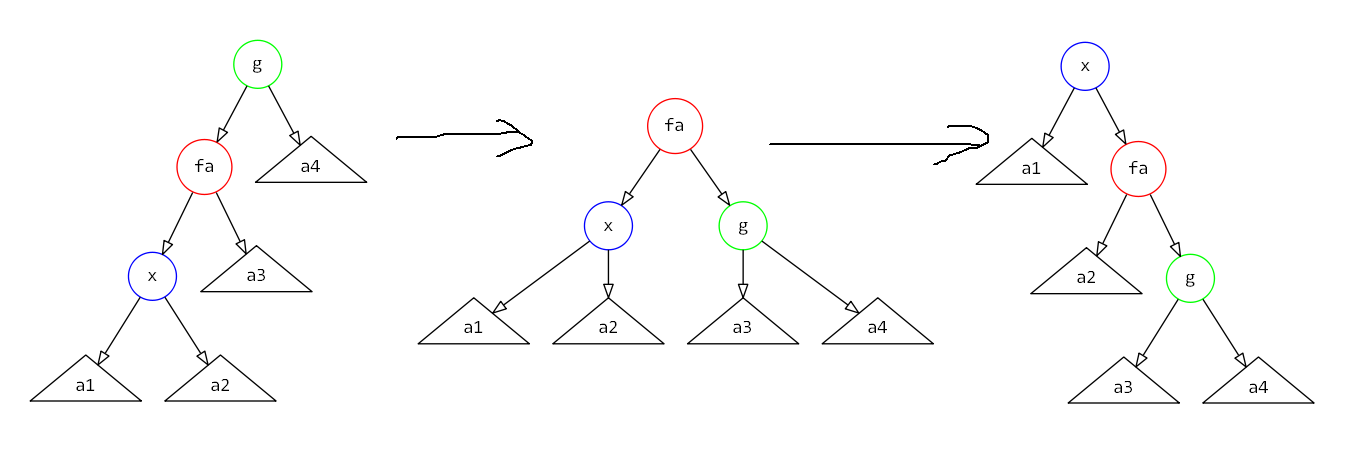
势能变化量为\(1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g)\)（缩小了常数的影响，但不能无视）

\(\leq 1 + w'(fa) + w'(g) - w(x) - w(fa) \leq 1 + w'(x) + w'(g) - 2w(x)\)

这是神仙复杂度证明中非常神奇的地方，通过一些有趣的性质，让常数项的代价合并到了势能的变化中

我们不妨设\(a = w'(g), b = w(x)\)，那么注意到\(w'(x) = a + b + 1\)

由于$2w'(x) - w'(g) - w(x) = \left \lceil \log_2 (a + b + 1) \right \rceil - \left \lceil \log_2 a \right \rceil + \left \lceil \log_2 a + b + 1 \right \rceil - \left \lceil \log_2 b \right \rceil $

注意到\(a, b\)在上式中是对称的，不妨设\(a \geq b\)

\(\geq \left \lceil \log_2 (a + b + 1) \right \rceil - \left \lceil \log_2 b \right \rceil \geq \left \lceil \log_2 (2b + 1) \right \rceil - \left \lceil \log_2 b \right \rceil \geq \left \lceil \log_2 b \right \rceil + 1 - \left \lceil \log_2 b \right \rceil \geq 1\)

因此有\(1 \leq 2w'(x) - w'(g) - w(x)\)，我们将\(1 + w'(x) + w'(g) - 2w(x)\)中的\(1\)放缩，可以得到

\(\leq 3(w'(x) - w(x))\)

---

\(zig-zag\)操作

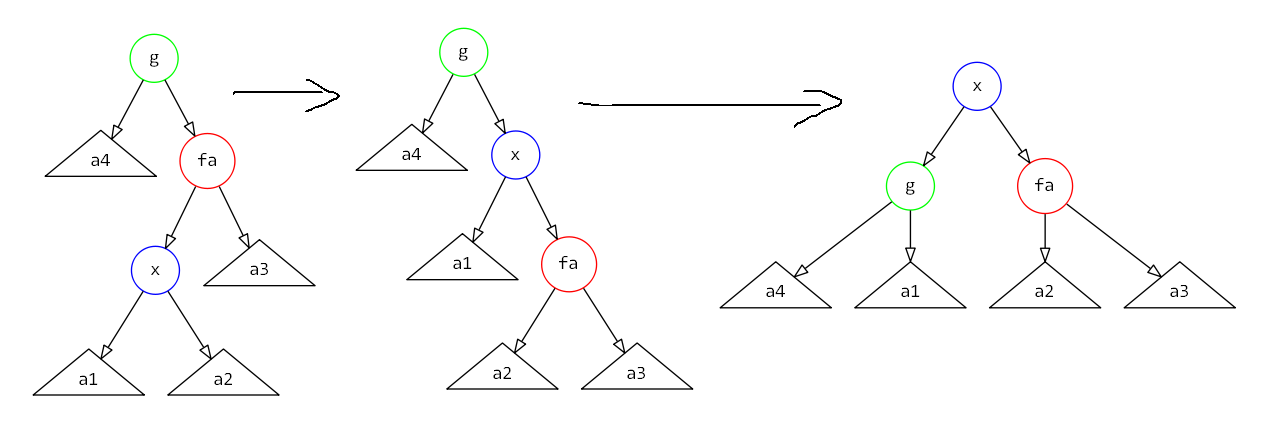
势能变化量为\(1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g) \leq 1 + w'(fa) + w'(g) - w(x) - w(fa) \leq 1 + w'(g) + w'(fa) - 2w(x)\)

由上文的结论，我们知道这里可以把\(1\)放缩成\(1 \leq 2w'(x) - w'(g) - w'(fa)\)

因此\(\leq 2(w'(x) - w(x))\)

---

把以上三种操作的势能全部放缩为\(\leq 3(w'(x) - w(x))\)

不妨假设\(splay\)一次，依次访问了点\(x_1, x_2 ... x_n\)，最后\(x_1\)会成为新的根

那么，最后的势能实际上是\(3(w'(x_1) - w(x_1) + w''(x_1) - w'(x_1) + .... + w(n) - w^{'''.....}(x_1)) + 1 = 3 * (w(n) - w(x_1)) + 1\leq log_2 n\)

因此，\(\varphi(m) - \varphi(m - 1) + \varphi(m - 1) - \varphi(m - 2) ... + \varphi(1) - \varphi(0) + \varphi(0) = n \log n + m \log n\)

即\(n\)个点的\(splay\)，做\(m\)次\(splay\)操作，复杂度为\(O(n \log n + m \log n)\)

---

\(LCT\)的复杂度分析

不咕了....

\(LCT\)的所有操作可以看做只有\(access\)操作，其他都是常数

那么\(access\)操作一共有两部分

• 在\(splay\)中走的复杂度

• 访问虚边的复杂度

---

首先是在\(splay\)中走的复杂度

定义\(w(x) = \left \lceil \log_2 (size(x)) \right \rceil\)，\(size(x)\)指\(x\)的所有虚边和实边的子树大小的和

我们定义势能函数为\(\varphi = \sum w(x)\)

不妨设它依次访问了\(x_1, x_2 ..., x_p\)

那么，类似上文\(splay\)的复杂度分析，我们可以得到总的一次势能变化量为\(-w(x_1) +w(x_2) - w(x_2) + w(x_3) ... +w(x_p) + 1\leq w(x_p) + 1 = O(\log n)\)

这也就是\(splay\)的\(finger-search\)的性质

初始势能为\(n \log n\)，因此这一部分的复杂度为\(O(n\log n + m \log n)\)

---

访问虚边的复杂度

我们定义势能函数\(\phi\)，为所有重虚边（儿子的子树大小大于等于自己的二分之一的虚边）的数量

那么，每次访问至多走\(\log\)条轻虚边，也就至多带来\(\log\)条重虚边，也就是以\(O(\log)\)的代价增加\(\log\)的势能

而每次访问一条重虚边就需要付出\(O(1)\)的代价来减小\(1\)的势能，并且访问完重虚边之后，不会有新的重虚边产生

因此，最终的复杂度是初始势能和势能变化量（实际操作的代价和势能变化量相同）的和，也就是\(O(n + m \log n)\)

---

因此，\(LCT\)的复杂度为\(O(n \log n + m \log n)\)