【洛谷】3953：逛公园【反向最短路】【记忆化搜索（DP）统计方案】

P3953 逛公园

题目描述

策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图，且没有 自环和重边。其中1号点是公园的入口，N号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从1号点进去，从N号点出来。

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d，那么策策只会喜欢长度不超过d+K的路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对P取模。

如果有无穷多条合法的路线，请输出−1。

输入输出格式

输入格式：

第一行包含一个整数 T, 代表数据组数。

接下来T组数据，对于每组数据： 第一行包含四个整数 N,M,K,P，每两个整数之间用一个空格隔开。

接下来M行，每行三个整数ai​,bi​,ci​，代表编号为ai​,bi​的点之间有一条权值为 ci​的有向边，每两个整数之间用一个空格隔开。

输出格式：

输出文件包含 T 行，每行一个整数代表答案。

输入输出样例

输入样例#1： 复制

2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0

输出样例#1： 复制

3
-1

说明

【样例解释1】

对于第一组数据，最短路为 3。 1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5为 33 条合法路径。

【测试数据与约定】

对于不同的测试点，我们约定各种参数的规模不会超过如下

测试点编号	T	N	M	K	是否有0边
1	5	5	10	0	否
2	5	1000	2000	0	否
3	5	1000	2000	50	否
4	5	1000	2000	50	否
5	5	1000	2000	50	否
6	5	1000	2000	50	是
7	5	100000	200000	0	否
8	3	100000	200000	50	否
9	3	100000	200000	50	是
10	3	100000	200000	50	是

对于 100%的数据, 1≤P≤109,1≤ai​,bi​≤N,0≤ci​≤1000。

数据保证：至少存在一条合法的路线。

---

被誉为是noip2017最难的一道题了...以前写过，但那时基本就是对着标程抄，还没有理解。

对记忆化搜索本来做得不好，希望能有一些更深入的理解了吧....

首先观察数据范围，明显是一道与$K$有关的DP。可以想到定义$dp[u][k]$表示$u$到$n$的距离是$dis[u]+k$的方案数。所以答案就是$\sum_{i=0}^{k}{dp[1][i]}$所以还要建反向边预处理出每个点到$n$的最短路$dis$。

然后发现，正向跑时，$dp[u][k]$可以从所有它可以到达的$v$更新过来。

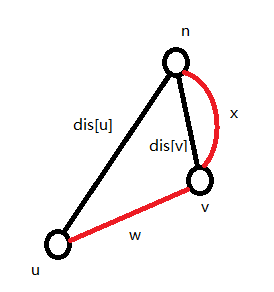
如图，已经确定了在$u$点时多出的$k$，那么如果要走到$v$点，可以确定$v$点多出的$k'$，通过$x+w-dis[u]=k$和$x-dis[v]=k'$可得出$k'=dis[u]+k-w-dis[v]$，然后就可以往下记忆化搜索来更新$dis[u][k]$了。初值$dp[u][0]=1$。

如何判0环？我们在搜索的时候定一个$fl[u][k]$标记，如果正在搜索中$fl=1$，如果搜索完了$fl=2$，如果同一个状态$[u][k]$第二次搜到的时候还在搜索中，即$fl[u][k]=1$，那么搜索过程中出现了0环，直接打标记退出即可。

#include<bits/stdc++.h>
using namespace std;

int n, p, m, k;

struct Node {
    int v, nex, w;
    Node(int v = , int nex = , int w = ) :
        v(v), nex(nex), w(w) { }
} Edge[];

int h[], stot;
void add(int u, int v, int w) {
    Edge[++stot] = Node(v, h[u], w);
    h[u] = stot;
}

int dis[], vis[];
void Spfa() {
    queue < int > q;
    memset(vis, , sizeof(vis));
    memset(dis, 0x3f3f3f3f, sizeof(dis));
    q.push(n); vis[n] = ; dis[n] = ;
    while(!q.empty()) {
        int u = q.front(); q.pop(); vis[u] = ;
        for(int i = h[u]; i; i = Edge[i].nex) {
            int v = Edge[i].v;
            if(dis[v] > dis[u] + Edge[i].w) {
                dis[v] = dis[u] + Edge[i].w;
                if(!vis[v])    vis[v] = , q.push(v);
            }
        }
    }
}

int dp[][];
int fl[][], flag;
int dfs(int u, int k) {
    if(fl[u][k] ==  || flag == -)    return flag = -;
    if(fl[u][k] == )    return dp[u][k];
    fl[u][k] = ;
    for(int i = h[u]; i; i = Edge[i].nex) {
        int v = Edge[i].v;
        int to = dis[u] + k - Edge[i].w - dis[v];
        if(to > k || to < )    continue;
        dp[u][k] = (dp[u][k] + dfs(v, to)) % p;
        if(flag == -)    return -;
    }
    fl[u][k] = ;
    return dp[u][k];
}

int a[], b[], c[];
int main() {
    int T;
    scanf("%d", &T);
    while(T --) {
        memset(h, , sizeof(h));    stot = ;
        flag = ;
        scanf("%d%d%d%d", &n, &m, &k, &p);
        for(int i = ; i <= m; i ++) {
            scanf("%d%d%d", &a[i], &b[i], &c[i]);
            add(b[i], a[i], c[i]);
        }
        Spfa();
        memset(h, , sizeof(h));    stot = ;
        for(int i = ; i <= m; i ++)
            add(a[i], b[i], c[i]);
        int ans = ;
        memset(fl, , sizeof(fl));
        memset(dp, , sizeof(dp));
        dp[n][] = ;
        for(int i = ; i <= k; i ++)
            ans = (long long)(ans + dfs(, i)) % p;
        if(~flag)    printf("%d\n", ans);
        else        printf("-1\n");
    }
    return ;
}