hihoCoder #1185 : 连通性·三(强联通分量+拓扑排序)

#1185 : 连通性·三

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

暑假到了!!小Hi和小Ho为了体验生活，来到了住在大草原的约翰家。今天一大早，约翰因为有事要出去，就拜托小Hi和小Ho忙帮放牧。

约翰家一共有N个草场，每个草场有容量为W[i]的牧草，N个草场之间有M条单向的路径。

小Hi和小Ho需要将牛羊群赶到草场上，当他们吃完一个草场牧草后，继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后，小hi和小Ho就把牛羊群赶回家。

一开始小Hi和小Ho在1号草场，在回家之前，牛羊群最多能吃掉多少牧草？

举个例子：

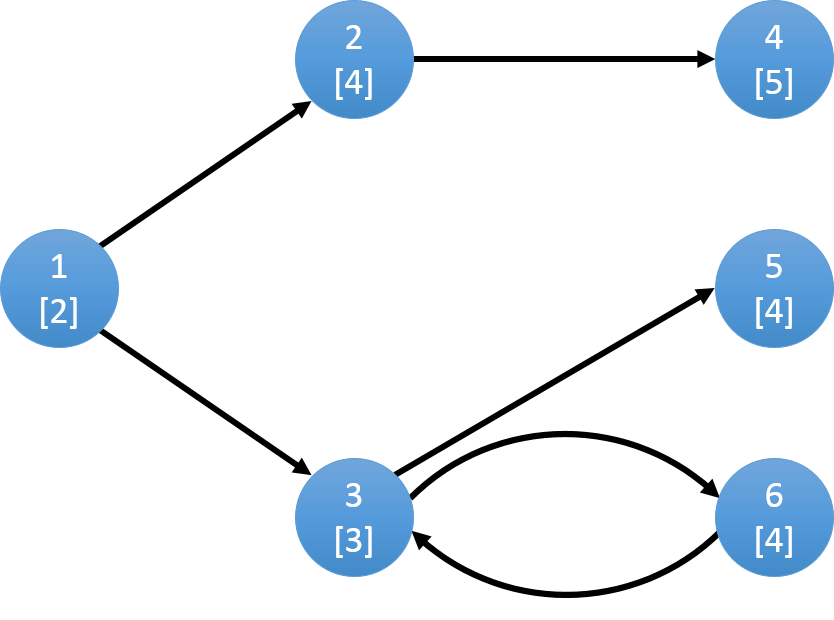
图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。

在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：

吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。

若选择从1到3，则可以到达5，6：

选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。

所以该图可以选择的路线有3条：

1->2->4 		total: 11
1->3->5 		total: 9
1->3->6->3->5: 		total: 13
  

所以最多能够吃到的牧草数量为13。

本题改编自USACO月赛金组

提示：强连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000

第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N

输出

第1行：1个整数，最多能够吃到的牧草数量。

代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<algorithm>
 using namespace std;
 const int N=2e4+;

 vector<int>v[N];
 vector<int>gra[N];
 stack<int>sk;
 int n,m,cnt,num,ans;
 int val[N],low[N],dfn[N],fa[N],sum[N],indeg[N],dp[N];
 bool vis[N];

 //求出强连通分量
 void tarjan(int u){
     low[u]=dfn[u]=++cnt;
     sk.push(u);
     for(int i=;i<v[u].size();i++){
         int t=v[u][i];
         if(!dfn[t]){
             tarjan(t);
             low[u]=min(low[u],low[t]);
         }
         else if(!fa[t]) low[u]=min(low[u],dfn[t]);
     }
     if(low[u]==dfn[u]){
         num++;
         while(!sk.empty()){
             int t=sk.top();
             sk.pop();
             fa[t]=num;
             sum[num]+=val[t];
             if(t==u) break;
         }
     }
 }

 //拓扑排序求最大价值
 int topo(){
     queue<int>q;
     for(int i=;i<=num;i++){
         if(indeg[i]==)
             q.push(i);
     }
     int ans=;
     while(!q.empty()){
         int k=q.front();
         q.pop();
         dp[k]+=sum[k];
         ans=max(dp[k],ans);
         for(int i=;i<gra[k].size();i++){
             int t=gra[k][i];
             indeg[t]--;
             dp[t]=max(dp[t],dp[k]);
             if(indeg[t]==)
                 q.push(t);
         }
     }
     return ans;
 }

 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%d",&val[i]);
     for(int i=;i<=m;i++){
         int a,b;
         scanf("%d%d",&a,&b);
         v[a].push_back(b);
     }
     tarjan();                  //起点是1
     //建新图
     for(int i=;i<=n;i++){
         if(fa[i]==) continue;
         for(int j=;j<v[i].size();j++){
             int t=v[i][j];
             if(fa[i]!=fa[t])
                 gra[fa[i]].push_back(fa[t]);
         }
     }
     //计算入度
     for(int i=;i<=num;i++){
         for(int j=;j<gra[i].size();j++){
             int t=gra[i][j];
             indeg[t]++;
         }
     }
     //利用拓扑排序算出答案
     printf("%d\n",topo());
     return ;
 }