Gauss Prime UVA - 1415

题意：给出a和b判定是否为高斯素数

解析：

普通的高斯整数i = sqrt(-1)

高斯整数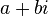是素数当且仅当：

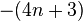a、b中有一个是零，另一个是形为或其相反数的素数；

或a、b均不为零，而为素数。

这题 提取出sqrt(2) 就和普通情况一样了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef long long ll;
using namespace std;

int main() {
    int t, a, b;
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d", &a, &b);
        int ok = ;
        if(a ==  || b ==)
        {
            if(a ==  && b == )
            {
                cout<< "No" <<endl;
                continue;
            }
            int temp;
            if(a == )
                temp = b;
            else
                temp = a;
            if(temp%)
            {
                cout<< "No" <<endl;
                continue;
            }
            else
            {
                temp -= ;
                for(int i=; i<=sqrt(temp + 0.5); i++)
                    if(temp % i == )
                    {
                        cout<< "No" <<endl;
                        ok = ;
                        break;
                    }
                if(!ok) printf("Yes\n");
            }

        }
        else
        {
            int flag = ;
            ll x = a*a + *b*b;
            for (int i = ; i <= sqrt(x+0.5); i++)
                if (x % i == ) {
                    printf("No\n");
                    flag = ;
                    break;
                }
            if (!flag)
                printf("Yes\n");
        }

    }
    return ;
}