【LeetCode371】 Sum of Two Integers
题目描述:

解题思路:
此题是要在不用操作符+和-的情况下,求两个整数的和。既然不能用内置的加减法,那就只能用位运算(&, |, ~, ^)。
(1)异或(xor):异或的数学符号为“⊕”,计算机符号为“xor”。
异或也叫半加运算,其运算法则相当于不带进位的二进制加法:异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(相同为0,不同为1),这些法则与加法是相同的,只是不带进位。
|
输入
|
运算符
|
输入
|
结果
|
|
1
|
⊕
|
0
|
1
|
|
1
|
⊕
|
1
|
0
|
|
0
|
⊕
|
0
|
0
|
|
0
|
⊕
|
1
|
1
|
(2)与(&):与运算后值为1的位即需要进位的位置,用与运算和移位的方法实现进位。
|
第一个输入
|
第二个输入
|
输出结果
|
|
1
|
1
|
1
|
|
1
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
0
|
所以,两个二进制整数 a 和 b,如果相加的过程中如果没有进位,那么 a+b=a⊕b,这里 ⊕ 表示异或。那么 a+b 的进位为多少呢,只有 1+1时才会出现进位。
所以 a+b 的进位可以表示为 2×(a & b),这里 & 表示两个数字的按位与运算。之所以要乘以 2,是因为要向上进一位(即左移一位)。
概括如下:
已知实现两个整数相加,可以分为两个步骤:
第一:不带进位相加,用异或实现。
第二:用上面的结果加上进位,用与运算和移位实现。又因为相加不能用+实现,所以此一步的相加仍得用两步实现,以此类推。
以5加7为例:
(1)没有进位的加:异或

(2)进位:需要在从左边数第一、第三位进位,即carry=a&b=0101中为1的位,需要进位多少呢,需要将0101左移一位得1010,也就是十进制的10,即(a&b)<<1=1010。
所以最后结果是0010+1010。
由于不能使用+,这里把0010当作a,把1010当作b,继续重复上面(1)(2)两个步骤,直到最后没有进位,异或的结果即为最终结果。
Java代码:
public class LeetCode371 {
public static void main(String[] args) {
int a=5,b=5;
System.out.println(a+"和"+b+"相加的结果是:"+new Solution().getSum(a, b));
}
}
class Solution {
public int getSum(int a, int b) {
int value=a^b;//没有进位的相加
int carry=a&b;//进位
int value_new;
while(carry!=0){
carry=carry<<1;
value_new=carry^value;
carry=carry&value;
value=value_new;
}
return value;
}
}
程序结果:
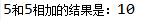
【LeetCode371】 Sum of Two Integers的更多相关文章
- 【LeetCode】Sum of Two Integers
问题描述: Calculate the sum of two integers a and b, but you are not allowed to use the operator + and - ...
- 【leetcode74】Sum of Two Integers(不用+,-求两数之和)
题目描述: 不用+,-求两个数的和 原文描述: Calculate the sum of two integers a and b, but you are not allowed to use th ...
- 【BZOJ3944】Sum(杜教筛)
[BZOJ3944]Sum(杜教筛) 题面 求\[\sum_{i=1}^n\mu(i)和\sum_{i=1}^n\phi(i)\] 范围:\(n<2^{31}\) 令\[S(n)=\sum_{i ...
- 【CF914G】Sum the Fibonacci 快速??变换模板
[CF914G]Sum the Fibonacci 题解:给你一个长度为n的数组s.定义五元组(a,b,c,d,e)是合法的当且仅当: 1. $1\le a,b,c,d,e\le n$2. $(s_a ...
- 【BZOJ4262】Sum 单调栈+线段树
[BZOJ4262]Sum Description Input 第一行一个数 t,表示询问组数. 第一行一个数 t,表示询问组数. 接下来 t 行,每行四个数 l_1, r_1, l_2, r_2. ...
- 【POJ1707】【伯努利数】Sum of powers
Description A young schoolboy would like to calculate the sum for some fixed natural k and different ...
- 【Leetcode 371】Sum of Two Integers
问题描述:不使用+是或-操作符进行整数的加法运算 int getSum(int a, int b); 我的思路:把整数化成二进制进行运算,注意类型是int,也就是要考虑负数.关于负数的二进制表示可见之 ...
- 【loj6059】Sum
Portal --> loj6059 Solution 看过去第一反应是..大力数位dp!然后看了一眼数据范围... 但是这没有什么关系!注意到我们不需要考虑前导零了,可以直接快乐dp ...
- 【leetcode】Sum Root to Leaf Numbers(hard)
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number ...
随机推荐
- CSS的设计模式
什么是设计模式? 曾有人调侃,设计模式是工程师用于跟别人显摆的,显得高大上:也曾有人这么说,不是设计模式没用,是你还没有到能懂它,会用它的时候. 先来看一下比较官方的解释:“设计模式(Design p ...
- 2018-10-15 21:07:38 c language
2018-10-15 21:07:38 c language C语言编译器,神奇的魔法师 在类 UNIX 系统(Linux.Mac OS 等)下,可执行程序没有特定的后缀,系统根据文件的头部信息来判断 ...
- Android使用ToolBar+DrawerLayout+NavigationView实现侧滑抽屉效果
学会使用DrawerLayout 学会使用NavigationView 学会使用ToolBar+DrawerLayout+NavigationView实现侧滑抽屉效果 学会实现Toolbar在顶部以及 ...
- android 自定义控件之ViewGroup生命周期执行步骤
前言 了解ViewGroup的生命周期的执行步骤对于自己自定义ViewGroup的时候十分重要,清楚了整个流程才能对ViewGroup有更深的理解.本文从个人的总结,来阐述一下执行的顺序.执行说明 首 ...
- spring <context:annotation-config/> 注解作用
<context:component-scan>包含<context:annotation-config/>的作用 <context:annotation-config/ ...
- [翻译] DDExpandableButton
DDExpandableButton https://github.com/ddebin/DDExpandableButton Purpose - 目的 DDExpandableButton is a ...
- 下拉刷新对象RefreshObject
下拉刷新对象RefreshObject 效果 说明 1. 分离了动画实现与刷新逻辑 2. 你可以根据自己的需要,设计自己的动画效果,你的动画只需要继承协议,实现协议里面的方法即可 3. 本设计方案是用 ...
- 重置 Winsock:初始化计算机网络环境
初始化网络环境,以解决由于软件冲突.病毒原因造成的参数错误问题(复杂网络环境下慎用).批处理代码: netsh winhttp reset proxy netsh winhttp reset trac ...
- Sublime Text 3 调用cmd运行c、java、python、batch file
一.调用cmd运行c(首先复制MinGW到C盘根目录,并添加环境变量) Tools --> Build System --> New Build System 删除所有内容 复制如下代码进 ...
- 设计一套砝码要求能称量出1 ~ 100g之间的任意重量,请问至少需要多少个砝码?以及每个砝码各自的重量是多少?
解析: 1g => 1g 2g => 1g 1g => 1 ~ 2g之间的重量 => 1g 2g => 1 ~ 3g之间的重量 4g => 1g 2g 1g =&g ...
