【poj3693】 Maximum repetition substring

http://poj.org/problem?id=3693 (题目链接)

题意

　　给定一个字符串，求重复次数最多的连续重复子串，若存在多组解，输出字典序最小的。

Solution

　　后缀数组论文题，就是加了个字典序要求。

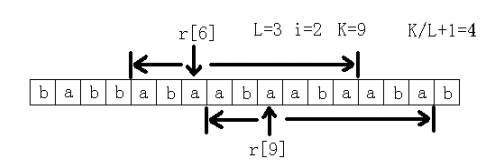
　　先穷举长度 L，然后求长度为 L 的子串最多能连续出现几次。首先连续出现 1 次是肯定可以的，所以这里只考虑至少 2 次的情况。假设在原字符串中连续出 现 2 次，记这个子字符串为 S，那么 S 肯定包括了字符 r[0], r[L], r[L*2], r[L*3], ……中的某相邻的两个。所以只须看字符 r[L*i]和 r[L*(i+1)]往前和 往后各能匹配到多远，记这个总长度为 K，那么这里连续出现了 K/L+1 次。最后 看最大值是多少。如图：

　　穷举长度 L 的时间是 n，每次计算的时间是 n/L。所以整个做法的时间复杂 度是 O(n/1+n/2+n/3+……+n/n)=O(nlogn)。

　　正着求一遍sa就可以算出r，反着求一遍sa就可以算出l。

　　对于字典序最小，我们考虑求出一个连续段以后，如果它的两端没有被卡死，也就是说它仍然可以在一定的区间内滑动，我们可以通过后缀的排名取到字典序最小的那个。这个操作可以用ST表维护。

　　于是就要写2个后缀数组，3个ST表，mdzz题→_→

细节

　　一个很重要的细节，反向字符串赋值的时候，要把第n+1位清为0，不然求后缀数组的时候会出问题。

　　为什么我ST表总是写错→_→

代码

// poj3693
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#define LL long long
#define inf 1<<30
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;

const int maxn=100010;
char s1[maxn],s2[maxn];
int sa1[maxn],sa2[maxn],rank1[maxn],rank2[maxn],height1[maxn],height2[maxn];
int bin[30],Log[maxn],st1[maxn][30],st2[maxn][30],str[maxn][30];

namespace Suffix {
	int wa[maxn],wb[maxn],ww[maxn];
	bool cmp(int *r,int a,int b,int l) {
		return r[a]==r[b] && r[a+l]==r[b+l];
	}
	void da(char *r,int *sa,int n,int m) {
		int i,j,p,*x=wa,*y=wb;
		for (i=0;i<=m;i++) ww[i]=0;
		for (i=1;i<=n;i++) ww[x[i]=r[i]]++;
		for (i=1;i<=m;i++) ww[i]+=ww[i-1];
		for (i=n;i>=1;i--) sa[ww[x[i]]--]=i;
		for (p=0,j=1;p<n;j*=2,m=p) {
			for (p=0,i=n-j+1;i<=n;i++) y[++p]=i;
			for (i=1;i<=n;i++) if (sa[i]>j) y[++p]=sa[i]-j;
			for (i=0;i<=m;i++) ww[i]=0;
			for (i=1;i<=n;i++) ww[x[y[i]]]++;
			for (i=1;i<=m;i++) ww[i]+=ww[i-1];
			for (i=n;i>=1;i--) sa[ww[x[y[i]]]--]=y[i];
			for (swap(x,y),p=x[sa[1]]=1,i=2;i<=n;i++)
				x[sa[i]]=cmp(y,sa[i-1],sa[i],j) ? p : ++p;
		}
	}
	void calheight(char *r,int *sa,int *height,int *rank,int n) {
		for (int i=1;i<=n;i++) rank[sa[i]]=i;
		for (int k=0,i=1;i<=n;i++) {
			if (k) k--;
			int j=sa[rank[i]-1];
			while (r[i+k]==r[j+k]) k++;
			height[rank[i]]=k;
		}
	}
}
int query1(int x,int y) {
	if (x>y) swap(x,y);x++;
	int k=Log[y-x+1];
	return min(st1[x][k],st1[y-bin[k]+1][k]);
}
int query2(int x,int y) {
	if (x>y) swap(x,y);x++;
	int k=Log[y-x+1];
	return min(st2[x][k],st2[y-bin[k]+1][k]);
}
int minr(int x,int y) {
	return rank1[x]<rank1[y] ? x : y;
}
int queryr(int x,int y) {
	int k=Log[y-x+1];
	return minr(str[x][k],str[y-bin[k]+1][k]);
}
int main() {
	int Case=0;
	bin[0]=1;for (int i=1;i<=20;i++) bin[i]=bin[i-1]<<1;
	for (int i=2;i<=100000;i++) Log[i]=Log[i>>1]+1;
	using namespace Suffix;
	while (scanf("%s",s1+1)!=EOF && s1[1]!='#') {
		int n=strlen(s1+1);
		s2[n+1]='\0';   //important
		for (int i=1;i<=n;i++) s2[n-i+1]=s1[i];
		da(s1,sa1,n,300);
		da(s2,sa2,n,300);
		calheight(s1,sa1,height1,rank1,n);
		calheight(s2,sa2,height2,rank2,n);
		for (int i=1;i<=n;i++) st1[i][0]=height1[i],st2[i][0]=height2[i];
		for (int i=1;i<=n;i++) str[i][0]=i;
		for (int j=1;j<=20;j++)
			for (int i=1;i+bin[j]<=n+1;i++) {
				st1[i][j]=min(st1[i][j-1],st1[i+bin[j-1]][j-1]);
				st2[i][j]=min(st2[i][j-1],st2[i+bin[j-1]][j-1]);
				str[i][j]=minr(str[i][j-1],str[i+bin[j-1]][j-1]);
			}
		int ansl=1,ansr=1,cnt=1;
		for (int i=2;i<=n;i++) if (s1[i]<s1[ansl]) ansl=ansr=i;
		for (int k=1;k<=n;k++)
			for (int i=1;i*k+1<=n;i++) {
				int x=(i-1)*k+1,y=i*k+1;
				int r=query1(rank1[x],rank1[y]);
				int l=query2(rank2[n-x+1],rank2[n-y+1]);
				int K=r+l+k-1;
				if (K/k>=cnt && K/k>1) {
					int s=queryr(x-l+1,x-l+1+K%k);
					if (K/k==cnt) s=minr(s,ansl);
					ansl=s,ansr=s+K/k*k-1;cnt=K/k;
				}
			}
		printf("Case %d: ",++Case);
		for (int i=ansl;i<=ansr;i++)
			printf("%c",s1[i]);
		puts("");
	}
    return 0;
}