AGC 018E.Sightseeing Plan——网格路径问题观止

原题链接

鸣谢：AGC 018E.Sightseeing Plan(组合 DP)

本蒟蒻认为，本题堪称网格路径问题观止。

因为涵盖了不少网格路径问题的处理方法和思路。

一句话题意：

给你三个矩形。

三个矩形从左下到右上排开。矩形顶点坐标范围是1e6

• 1≤X₁≤X₂<X₃≤X₄<X₅≤X₆≤10⁶
• 1≤Y₁≤Y₂<Y₃≤Y₄<Y₅≤Y₆≤10⁶

大概就是这样：

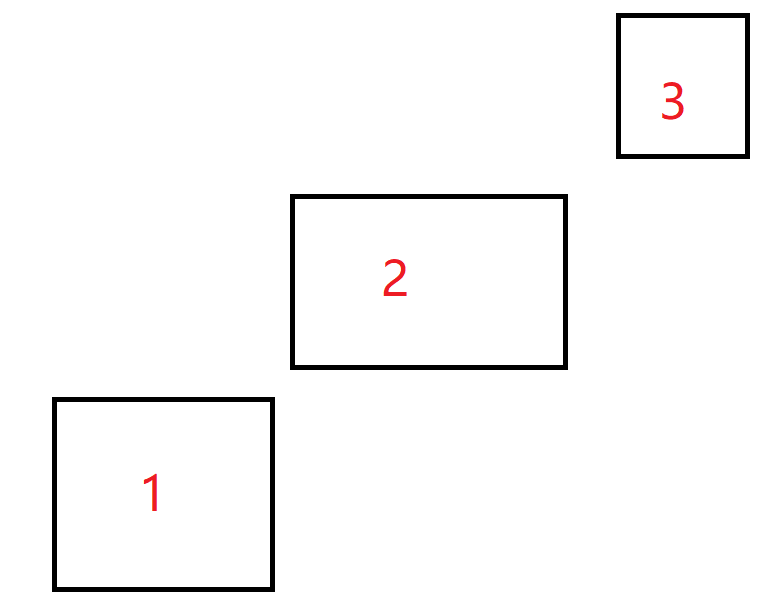
对于所有的1中选择一个点P1，2中选择一个点P2，3中选择一个点P3。

求从P1到P2再到P3的最短路径条数之和。

从一个矩形再到另外一个矩形还要经过一个矩形太复杂。我们化简情况处理下。

反正本质就是所有三个点之间的路径。

一、一个点到一个点

你必须要知道的：

从(x1,y1)到(x2,y2)的最短路径，就是只能往上或者往右走。

最短路径条数就是：C(x2-x1+y2-y1,x2-x1)

所以我们可以O(1000000^6)枚举

二、一个点到一个矩形

$F(x,y)$表示，从$(0,0)$到$(x,y)$的路径条数。

这个可以直接算。

发现，

$F(x,y)=\sum_{j=0}^yF(x-1,j)$

可以理解为，从原点到所有的$(x-1,j)$然后向上走一步，然后直接向右到达$(x,y)$

肯定不重不漏。

那么，可以得到：

从$(0,0)$到一个矩阵路径，就是：

$F(x2+1,y2+1)-F(x2+1,y1)-F(x1,y2+1)+F(x1,y1)$

就是一个小容斥。

用上面的$F(x,y)=\sum_{j=0}^yF(x-1,j)$

把$F(x2+1,y2+1)$还有$F(x1,y2+1)$展开消一消，

每次保留$F(x2+1,j)$和$F(x1,j)$往下消。

画画图就看出来了。

所以，我们得到了从一个点到一个矩阵的路径条数。

只要计算那四个点即可。

三、一个矩形到一个矩形

列出式子：

$G$示路径条数

$M_1$代表第一个矩形，$M_2$代表第二个矩形。

$\sum_{x1} \sum_{y1} \sum_{x2} \sum_{y2}G((x1,y1),(x2,y2))$

可以提出两个sigma

变成枚举一个点，求到另外一个矩形的方案数

$\sum_{x1} \sum_{y1}G((x1,y1),M_2)$

其实就是：

$\sum_{x1} \sum_{y1}\sum_{xx}\sum_{yy}(G((x1,y1),(xx,yy))$

$xx,yy$代表那四个关键点。（省略了四个关键点正负号）

反过来，每个关键点都会被$M_1$所有的点统计一次。

所以，一个关键点的贡献，就是这个关键点到$M_1$的路径条数。

就是这个关键点到$M_1$的四个关键点路径条数。（当然，要有正负号）

所以，一个矩形到一个矩形的路径条数，

就是两个矩形四个关键点分别进行条数计算。处理好符号即可。

四、一个矩形经过一个矩形再到另一个矩形

可以把三的结论推广。

就是，第一个矩形四个关键点，到第三个矩形四个关键点，然后路径上经过第二个矩形的方案数。

所以，$4\times 4$枚举第一第三个矩形的关键点的话，

问题就变成了从一个点出发，经过一个矩形再到另外一个点的方案数。

直接枚举还是$O(n^2)$的。

发现，经过第二个矩形，
必然要么从$(x,y3)$（下边界）要么从$(x3,y)$（左边界）
进入。

所以，我们枚举进入点。

进入这个点，就一定进入了这个矩形。再到终点的任意一条路径，都是合法的。

再乘上从起点到这个进入点的方案数就是这个进入点的贡献。

必然不重不漏地枚举完了所有的合法路径。

所以我们成功的A掉了这个题。

五、然鹅并没有做完。。。

发现，不是要求经过第二个矩形的路径条数啊，我们要在第二个矩形中选择一个点。。。。

一个经过第二个矩形的长度为$len$的路径，就对应着$len$个方案。（每个位置都可以作为$P_2$）

我们经常转化研究对象，尝试分开统计贡献。

分开统计的前提是，贡献必须可以处理成互不相关的形式。

这个可以不可以呢？

但是凉凉，这个$len$还和离开点有关。。。

难道只能$O(n^2)$枚举进入点和离开点？

不！我们还有方法！

一个$len$怎么计算？

进入点$(x1,y1)$,离开点$(x2,y2)$

有$len=x2-x1+y2-y1+1$

诶！！

$x1,x2,y1,y2$貌似可以分离！！

那么，我们可以枚举进入点。

贡献是：$(-1)\times$刚才的两个组合数$\times(x+y)$

离开点：

贡献是：$(+1)\times$刚才的两个组合数$\times(x+y)$

（其实这个也是不重不漏枚举了所有路径）

相加的话，

发现，对于每个合法的路径，恰好被计算了两遍。（进入离开点各一次）

第一遍把$-x1-y1$算上，

第二遍把$x2+y2+1$算上。

所以，每个合法路径贡献就是$len$次。和题意符合。

完结撒花！！！~~~

六、一些代码实现细节：

1.len的长度是：$(x2-x1+y2-y1+1)$别忘了$+1$

2.注意，矩阵矩阵的之间的路径，

根据推导，是先转化成$M_2$中关键点到$M_1$矩阵的路径，所以，$M_1$的矩阵的四个关键点分别是$(x1-1,y1-1),(x2,y1-1),(x1-1,y2),(x2,y2)$

类比之前，这个是从上往下走的，所以要这样处理。

#include<bits/stdc++.h>
#define ri register int
using namespace std;
typedef long long ll;
const int mod=1e9+;
const int N=2e6+;
ll ans=;
ll jie[N],ni[N];
struct node{
    int x,y,fl;
    void init(int a,int b,int c){
        x=a,y=b,fl=c;
    }
}p[];
int tot;
int x3,y3,x4,y4;
int xx[],yy[];
ll qm(ll x,ll y){
    ll ret=;
    while(y){
        if(y&) ret=ret*x%mod;
        x=x*x%mod;
        y>>=;
    }
    return ret;
}
ll C(int n,int m){
    return jie[n]*ni[m]%mod*ni[n-m]%mod;
}
ll G(int x1,int y1,int x2,int y2){
    ll A=abs(x2-x1),B=abs(y2-y1);
    return C(A+B,B);
}
ll sol(int x1,int y1,int x2,int y2,int f1,int f2){
    ll ret=;
    for(ri x=x3;x<=x4;++x){
        ret=(ret+G(x1,y1,x,y4)*G(x,y4+,x2,y2)%mod*(x+y4+))%mod;//注意这里的x+y4+1的+1
        ret=(ret-G(x1,y1,x,y3-)*G(x,y3,x2,y2)%mod*(x+y3)%mod+mod)%mod;
    }
    for(ri y=y3;y<=y4;++y){
        ret=(ret+G(x1,y1,x4,y)*G(x4+,y,x2,y2)%mod*(x4+y+))%mod;
        ret=(ret-G(x1,y1,x3-,y)*G(x3,y,x2,y2)%mod*(x3+y)%mod+mod)%mod;
    }
    ret=ret*(f1*f2);

    return ret;
}
int main(){
    int x,y;
    for(ri i=;i<=;++i)scanf("%d",&xx[i]);
    for(ri i=;i<=;++i)scanf("%d",&yy[i]);
    jie[]=;
    for(ri i=;i<=N-;++i) jie[i]=jie[i-]*i%mod;
    ni[N-]=qm(jie[N-],mod-);
    for(ri i=N-;i>=;--i) ni[i]=ni[i+]*(i+)%mod;

    x3=xx[],y3=yy[],x4=xx[],y4=yy[];
    p[].init(xx[]-,yy[]-,);p[].init(xx[],yy[]-,-);//注意这里是这样的
    p[].init(xx[]-,yy[],-);p[].init(xx[],yy[],);

    p[].init(xx[],yy[],);p[].init(xx[]+,yy[],-);
    p[].init(xx[],yy[]+,-);p[].init(xx[]+,yy[]+,);

    for(int i=;i<=;++i){
        for(int j=;j<=;++j){
            ans=(ans+sol(p[i].x,p[i].y,p[j].x,p[j].y,p[i].fl,p[j].fl)+mod)%mod;
        }
    }
    printf("%lld",ans);
    return ;
}

七、总结

我们成功地把一个O(n^6)变成了O(n)

思路就是化简问题，然后从简单到困难，利用之前的结论考虑，不断转化简化问题。

最后的差分len也是异常精彩。

组合数和路径条数的问题，经常是考虑一个物品的贡献。

可以尝试往这方面想。

这里也有有一个不错的路径组合意义转化题：fzyzojP3782 -组合数问题