HDU-1978How many ways

Problem Description

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

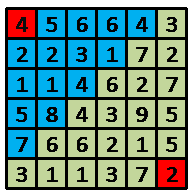
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

 

Sample Output

3948

---

思路：

比较简单的一道题目，遍历所有的邻接点，然后dfs设置好返回点就出来结果了

有个小技巧，即判断可到达点的范围时，可以先遍历所有的点，然后再进行筛选

PS，思路很简单，代码就不想说什么了

---

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
 
int n,m,dp[][],a[][];
 
int check(int x,int y)
{
    if(x< || x>n || y< || y>m)
        return ;
    return ;
}
 
int dfs(int x,int y)
{
    if(dp[x][y]>=) return dp[x][y];
    dp[x][y] = ;
    int i,j;
    for(i = ; i<=a[x][y]; i++)
        for(j = ; j<=a[x][y]-i; j++)
        {
            if(check(x+i,y+j))
                continue;
            dp[x][y] = (dp[x][y]+dfs(x+i,y+j))%;
        }
    return dp[x][y];
}
 
int main()
{
    int t,i,j;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(i = ; i<=n; i++)
            for(j = ; j<=m; j++)
                scanf("%d",&a[i][j]);
        memset(dp,-,sizeof(dp));
        dp[n][m] = ;
        printf("%d\n",dfs(,));
    }
 
    return ;
}