Fibonacci（数论 输出前四位Fibonacci）

Fibonacci

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 4221    Accepted Submission(s): 1954

Problem Description

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列 (f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。 接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

 

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

 

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

 

Sample Input

0
1
2
3
4
5
35
36
37
38
39
40

 

Sample Output

0
1
1
2
3
5
9227
1493
2415
3908
6324
1023

 

Author

daringQQ

题解：暴力了下果断超时了。。。网上查了个吊方法。。。。

题意:输出Fibonacci数组的前四位,n<=100000000;思路:

首先:看到这个题的数据范围,0(n)的时间复杂度是不行的。

然后想下数组可不可以用来储存呢?n<=100000000,数太大了,就算表示 ,也会超时。

再想是不是有循环节,但是前四位的是跟后面几位有关系的(可以产生进位),不能只存前四位;

最后想想:Fibonacci数肯定有公式可以求得公式如下:

• 思考如何产生前4位。

先看对数的性质,loga(b^c)=c*loga(b),loga(b*c)=loga(b)+loga(c);假设给出一个数10234432,

那么log10(10234432)=log10(1.0234432*10^7)【用科学记数法表示这个数】=log10(1.0234432)+7;

log10(1.0234432)就是log10(10234432)的小数部分.

log10(1.0234432)=0.010063744(取对数所产生的数一定是个小数)

再取一次幂:10^0.010063744=1.023443198

那么要取前几位就比较好想了吧。

对公式取对数:

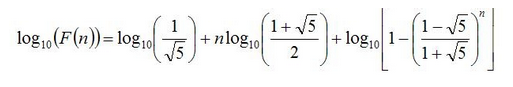
最后一项小于0并且很小可以不用计算

步骤:

先取对数(对10取),然后得到结果的小数部分bit,pow(10.0,bit)以后如果答案还是<1000那么就一直乘10。

处理前20位，是为了消除进位的影响；

ac代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
#define mem(x,y) memset(x,y,sizeof(x))
#define SI(x) scanf("%d",&x)
#define PI(x) printf("%d",x)
#define SD(x,y) scanf("%lf%lf",&x,&y)
#define P_ printf(" ")
int main(){
	int n;
	int dp[20]={0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181};
	while(~SI(n)){
		double ans=log10(1/sqrt(5.0))+n*log10((1+sqrt(5.0))/2.0);
		ans=ans-floor(ans);
		ans=pow(10,ans);
		if(n<20)printf("%d\n",dp[n]);
		else printf("%d\n",(int)(ans*1000));
	}
	return 0;
}

　　暴力超时代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
#define mem(x,y) memset(x,y,sizeof(x))
#define SI(x) scanf("%d",&x)
#define PI(x) printf("%d",x)
#define SD(x,y) scanf("%lf%lf",&x,&y)
#define P_ printf(" ")
const int MAXN=100010;
char c[MAXN];
int x[MAXN],y[MAXN],z[MAXN];
void bigsum(char *a,char *b){
	int len1=strlen(a),len2=strlen(b);
	int len=max(len1,len2);
	mem(x,0);mem(y,0);mem(z,0);
	for(int i=0,j=len1-1;i<len1;i++,j--)x[i]=a[j]-'0';
	for(int i=0,j=len2-1;i<len2;i++,j--)y[i]=b[j]-'0';
	for(int i=0;i<len;i++){
		z[i]=x[i]+y[i]+z[i];
		z[i+1]+=z[i]/10;
		z[i]%=10;
		if(z[len])len++;
	}
	for(int i=0,j=len-1;i<len;i++,j--)c[i]=z[j]+'0';
	c[len]='\0';
}
int main(){
	int n;
	char a[MAXN],b[MAXN];
	while(~SI(n)){
		if(n==0){
			puts("0");continue;
		}
		if(n==1){
			puts("1");continue;
		}
		if(n==2){
			puts("1");continue;
		}
			a[0]='1';a[1]='\0';
			c[0]='2',c[1]='\0';
		for(int i=3;i<n;i++){
			//puts(c);
			strcpy(b,c);
			bigsum(a,c);
			strcpy(a,b);
		}
		for(int i=0;i<4&&c[i];i++)printf("%c",c[i]);puts("");
	}
	return 0;
}

　　java:

package com.lanqiao.week1;

import java.util.Scanner;

public class hdoj1568 {
    private static Scanner cin;
    private static int MOD = 1000000007;
    static{
        cin = new Scanner(System.in);
    }
    public static void main(String[] args) {
        int n;
        int[] dp = {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 1094, 1771, 2865};
        //2584 4181 6765 10946 17711 28657
//        for(int i = 0; i < 10; i++){
//            System.out.print(" " + i + "-->" + dp[i]);
//        }
        while(cin.hasNext()){
            n = cin.nextInt();
            //System.out.println(n);
            if(n < dp.length){
                System.out.println(dp[n]);
            }else{
                double x =
                        Math.log10(1.0 / Math.sqrt(5.0))
                        + n * Math.log10((1.0 + Math.sqrt(5.0)) / 2.0);
                x = x - Math.floor(x);
                System.out.println((int)(Math.pow(10, x) * 1000));
            }

        }

    }
}