学习笔记——二叉树相关算法的实现（Java语言版）

二叉树遍历概念和算法

遍历（Traverse）：

　　所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。

　　从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。

　　因此，在任一给定结点上，可以按某种次序执行三个操作：

　　　　⑴ 访问结点本身（D），

　　　　⑵ 遍历该结点的左子树（L），

　　　　⑶ 遍历该结点的右子树（R）。

 

　　先序/根遍历DLR：根   左子树     右子树
　　中序/根遍历LDR：左子树   根     右子树
　　后根/序遍历LRD：左子树     右子树  根

 

　　注意：由于树的递归定义，其实对三种遍历的概念其实也是一个递归的描述过程

 

算法实现：

二叉树结点类

/**
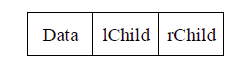
 * 二叉链表的结点
 * @author shangyang
 *
 */
public class Node {

    Object value;        // 结点值
    Node leftChild;        // 左子树的引用
    Node rightChild;    // 右子树的引用

    public Node(Object value) {
        super();
        this.value = value;
    }

    public Node(Object value, Node leftChild, Node rightChild) {
        super();
        this.value = value;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
    }

    @Override
    public String toString() {
        return "Node [value=" + value + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]";
    }
}

二叉树方法接口类

/**
 * 二叉树的接口
 * 可以有不同的实现类，每个类可以使用不同的存储结构，比如顺序结构、链式结构
 * @author shangyang
 *
 */
public interface BinaryTree {

    /**
     * 是否为空树
     */
    public boolean isEmpty();

    /**
     * 树结点数量
     */
    public int size();

    /**
     * 获取树的高度
     */
    public int getHeight();

    /**
     * 查询指定值的结点
     * @param value
     * @return
     */
    public Node findKey(Object value);

    /**
     * 前序递归遍历
     */
    public void preOrderTraverse();

    /**
     * 中序递归遍历
     */
    public void inOrderTraverse();

    /**
     * 后序递归遍历
     */
    public void postOrderTraverse();

    /**
     * 按照层次遍历（借助队列）
     */
    public void levelOrderByStack();

    /**
     * 中序非递归遍历
     */
    public void inOrderByStack();
}

二叉树接口类

实现二叉树接口类

创建树的根对象，并写出构造函数。

public class LinkedBinaryTree implements BinaryTree {

    private Node root;    // 根结点

    public LinkedBinaryTree() {
    }

    public LinkedBinaryTree(Node root) {
        this.root = root;
    }
}

创建二叉树

    // 创建一个二叉树
    Node nodeF = new Node("F",null,null);
    Node nodeE = new Node("E",null,null);
    Node nodeD = new Node("D",null,null);
    Node nodeC = new Node("C",nodeF,null);
    Node nodeB = new Node("B",nodeD,nodeE);
    Node nodeA = new Node("A",nodeB,nodeC);

    // 声明nodeA为根结点
    BinaryTree btree = new LinkedBinaryTree(nodeA);        

判断二叉树是否为空

为空返回true，不为空返回false

public boolean isEmpty() {
    return root == null;
}

输出二叉树结点数量

运用递归的思想，二叉树结点树 = 左子树结点数量 + 右子树结点数量 + 1

　　public int size() {
        System.out.println("二叉树结点数量： ");
        return this.size(root);
    }
    private int size(Node root) {
        if(root == null) {
            return 0;
        } else {
            // 获取左子树的数量
            int nl = this.size(root.leftChild);
            // 获取右子树的数量
            int nr = this.size(root.rightChild);
            // 返回左子树、右子树size之和并加1
            return nl + nr + 1;
        }
    }

二叉树的深度（高度）

如果二叉树为空，则其深度为0。

如果二叉树只有根结点，无左右子树，则其深度为1。

如果二叉树结点数大于1,则用递归的思想计算其深度。二叉树的深度 = 左右子树的最大深度 + 1。

    public int getHeight() {
        System.out.println("二叉树的高度是 ：");
        return this.getHeight(root);
    }
    private int getHeight(Node root) {
        if(root == null) {
            return 0;
        } else {
            // 获取左子树的高度
            int nl = this.getHeight(root.leftChild);
            // 获取右子树的高度
            int nr = this.getHeight(root.rightChild);
            // 返回左子树、右子树较大高度并加1
            return nl > nr ? nl + 1 : nr + 1;
        }
    }

在二叉树中查找某个值

运用递归的思想，将要查找的值逐个与根结点，根结点的左子树和右子树的值进行比较，并进行返回。

    public Node findKey(Object value) {
        return this.findKey(value,root);
    }
    private Node findKey(Object value,Node root) {
        // 结点为空，可能是整个树的根结点，也可能是递归调用中叶子结点中左孩子和右孩子
        if(root == null) {
            return null;
        } else if (root != null && root.value == value) {
            return root;
        } else {    // 递归体
            Node leftnode = this.findKey(value,root.leftChild);
            Node rightnode = this.findKey(value, root.rightChild);
            if(leftnode != null && leftnode.value == value) {
                return leftnode;
            } else if (rightnode != null && rightnode.value == value) {
                return rightnode;
            } else {
                return null;
            }
        }
    }

先序递归遍历

若二叉树非空，则依次执行如下操作：

　　⑴ 访问根结点；

　　⑵ 遍历左子树；

　　⑶ 遍历右子树。

    public void preOrderTraverse() {
        // 输出根结点的值
        if(root != null) {
            System.out.print(root.value + "  ");

            // 对左子树进行先序遍历
            // 构建一个二叉树，根是左子树的根
            BinaryTree leftTree = new LinkedBinaryTree(root.leftChild);
            leftTree.preOrderTraverse();

            // 对右子树进行先序遍历
            // 构建一个二叉树，根是左子树的根
            BinaryTree rightTree = new LinkedBinaryTree(root.rightChild);
            rightTree.preOrderTraverse();
        }
    }

中序递归遍历

若二叉树非空，则依次执行如下操作：

　　⑴ 遍历左子树；

　　⑵ 访问根结点；

　　⑶ 遍历右子树。

    public void inOrderTraverse() {
        System.out.println("中序遍历");
        this.inOrderTraverse(root);
        System.out.println();
    }
    private void inOrderTraverse(Node root) {
        if(root != null) {
            // 遍历左子树
            this.inOrderTraverse(root.leftChild);
            // 输出根的值
            System.out.print(root.value + "  ");
            // 遍历右子树
            this.inOrderTraverse(root.rightChild);
        }
    }

后续递归遍历

若二叉树非空，则依次执行如下操作：

　　⑴ 遍历左子树；

　　⑵ 遍历右子树；

　　⑶ 访问根结点。

    public void postOrderTraverse() {
        System.out.println("后序遍历");
        this.postOrderTraverse(root);
        System.out.println();
    }
    private void postOrderTraverse(Node root) {
        if(root != null) {
            // 遍历左子树
            this.postOrderTraverse(root.leftChild);
            // 遍历右子树
            this.postOrderTraverse(root.rightChild);
            // 输出根的值
            System.out.print(root.value + "  ");
        }
    }

按照层次遍历（借助队列）

按照从上到下、从左到右的次序进行遍历。先遍历完一层，再遍历下一层，因此又叫广度优先遍历。

该方法可以借助java中提供queue队列接口来完成。LinkedList实现了该接口。

    public void levelOrderByStack() {
        if(root == null)
            return;
        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        while(queue.size() != 0) {
            int len = queue.size();
            for(int i = 0; i < len; i++) {
                Node temp = queue.poll();
                System.out.print(temp.value + "  ");
                if(temp.leftChild != null)
                    queue.add(temp.leftChild);
                if(temp.rightChild != null)
                    queue.add(temp.rightChild);
            }
        }
    }

中序非递归遍历（借助栈）

（1) 若根结点不为空，则将其放如栈中，并判断其左子树是否为空。

（2) 若不为空，则将子树根结点放入栈中，并继续向下判断，直至左子树为空。

（3) 若栈中有结点，则将其取出，并对其右子树根结点进行（1)（2)步骤，直至无结点或栈中元素为空。

    public void inOrderByStack() {
        // 创建栈
        Deque<Node> stack = new LinkedList<Node>();
        Node current = root;
        while(current != null || !stack.isEmpty()) {
            while(current != null) {
                stack.push(current);
                current = current.leftChild;
            }

            if(!stack.isEmpty()) {
                current = stack.pop();
                System.out.print(current.value + " ");
                current = current.rightChild;
            }
        }
    }