边框回归（bounding-Box regression）

转自：https://blog.csdn.net/zijin0802034/article/details/77685438

• 为什么要边框回归？
• 什么是边框回归？
• 边框回归怎么做的？
• 边框回归为什么宽高，坐标会设计这种形式？
• 为什么边框回归只能微调，在离Ground Truth近的时候才能生效？

1、为什么要边框回归？

对于上图，绿色的框表示Ground Truth, 红色的框为Selective Search提取的Region Proposal。那么即便红色的框被分类器识别为飞机，但是由于红色的框定位不准(IoU<0.5)， 那么这张图相当于没有正确的检测出飞机。 如果我们能对红色的框进行微调， 使得经过微调后的窗口跟Ground Truth 更接近， 这样岂不是定位会更准确。 确实，Bounding-box regression 就是用来微调这个窗口的。
2、边框回归是什么？

对于窗口一般使用四维向量(x,y,w,h) 来表示， 分别表示窗口的中心点坐标和宽高。 对于图 2, 红色的框 P 代表原始的Proposal, 绿色的框 G 代表目标的 Ground Truth， 我们的目标是寻找一种关系使得输入原始的窗口 P 经过映射得到一个跟真实窗口 G 更接近的回归窗口G^G^。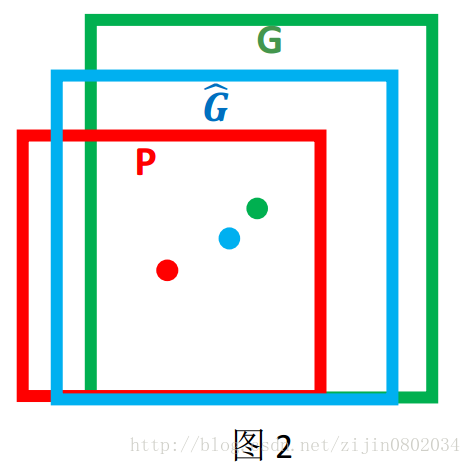

边框回归的目的既是：给定(Px,Py,Pw,Ph)寻找一种映射f， 使得f(Px,Py,Pw,Ph)=(Gx^,Gy^,Gw^,Gh^) 并且(Gx^,Gy^,Gw^,Gh^)≈(Gx,Gy,Gw,Gh)

3、边框回归是怎么做的？

那么经过何种变换才能从图 2 中的窗口 P 变为窗口G^G^呢？ 比较简单的思路就是: 平移+尺度放缩

4、为什么宽高尺度会设计这种形式？
这边我重点解释一下为什么设计的tx,tytx,ty为什么除以宽高，为什么tw,thtw,th会有log形式！！！

首先CNN具有尺度不变性， 以图3为例：

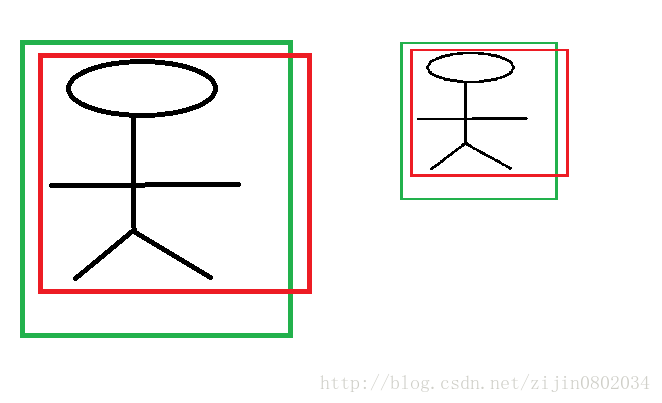
x,y 坐标除以宽高
上图的两个人具有不同的尺度，因为他都是人，我们得到的特征相同。假设我们得到的特征为ϕ1,ϕ2，那么一个完好的特征应该具备ϕ1=ϕ。ok，如果我们直接学习坐标差值，以x坐标为例，xi,pi分别代表第i个框的x坐标，学习到的映射为ff, f(ϕ1)=x1−p1，同理f(ϕ2)=x2−p2。从上图显而易见，x1−p1≠x2−p1。也就是说同一个x对应多个y，这明显不满足函数的定义。边框回归学习的是回归函数，然而你的目标却不满足函数定义，当然学习不到什么。

宽高坐标Log形式
我们想要得到一个放缩的尺度，也就是说这里限制尺度必须大于0。我们学习的tw,th怎么保证满足大于0呢？直观的想法就是EXP函数，如公式(3), (4)所示，那么反过来推导就是Log函数的来源了。

5、为什么IoU较大，认为是线性变换？
当输入的 Proposal 与 Ground Truth 相差较小时(RCNN 设置的是 IoU>0.6)， 可以认为这种变换是一种线性变换， 那么我们就可以用线性回归来建模对窗口进行微调， 否则会导致训练的回归模型不 work（当 Proposal跟 GT 离得较远，就是复杂的非线性问题了，此时用线性回归建模显然不合理）。这里我来解释：

Log函数明显不满足线性函数，但是为什么当Proposal 和Ground Truth相差较小的时候，就可以认为是一种线性变换呢？大家还记得这个公式不？参看高数1。

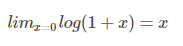
现在回过来看公式(8):

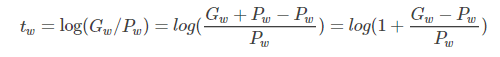
当且仅当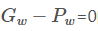的时候，才会是线性函数，也就是宽度和高度必须近似相等。