hdu3480 Division（dp平行四边形优化）

题意：将n个数分成m段，每段的代价为最大值减最小值的平方，为代价最小是多少n<=10000 ,m<=5000

题解：先拍好序，从小到大，这样绝对是花费最小的，不过怎么样来做呢？一定很容易想到dp

分段dp十分好想吧，f[i][j]表示前i个数，分成j个数的最小值。

w[i][j]区间包含性十分好证明，

平行四边不等性，可以很好证明，

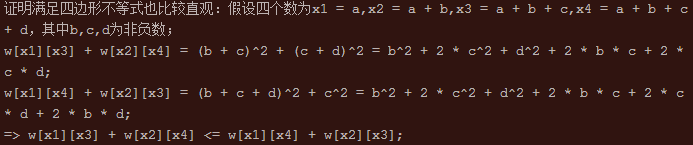
对吧，这样很好理解

所以得出f[i][j]满足------>s[i][j-1]<=s[i][j]<=s[i+1][j]

这个得出来就ok了，但是这道题有点奇葩，s[i][j-1]以前就求好了，但是s[i+1][j]呢？所以

需要倒着dp，先求s[i+1][j]在去搞s[i][j];

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #define inf 2000000009
 using namespace std;

 int cas,n,m,now=;
 int a[];
 int f[][],s[][];

 int main()
 {
     scanf("%d",&cas);
     while(cas--)
     {
         scanf("%d%d",&n,&m);
         for (int i=;i<=n;i++)
             scanf("%d",&a[i]);
         sort(a+,a+n+);
         for (int i=;i<=n;i++)
             f[i][]=(a[i]-a[])*(a[i]-a[]),s[i][]=;
         for (int k=;k<=m;k++)
         {
             s[n+][k]=n;
             for (int i=n;i>=k;i--)
             {
                 f[i][k]=inf;
                 for (int j=s[i][k-];j<=s[i+][k];j++)
                 {
                     int t=f[j-][k-]+(a[i]-a[j])*(a[i]-a[j]);
                     if (t<f[i][k]) f[i][k]=t,s[i][k]=j;
                 }
             }
         }
         printf("Case %d: %d\n",++now,f[n][m]);
     }
 }