[Codeforces]605E Intergalaxy Trips

　　小C比较棘手的概率期望题，感觉以后这样的题还会贴几道出来。

Description

　　给定一个n*n的邻接矩阵，邻接矩阵中元素pi,j表示的是从 i 到 j 这条单向道路在这一秒出现的概率百分比，走一条道路的时间需要1秒，问从1号点出发到n号点最短所需花费时间的期望。最短所需花费时间即在每一个点都按照最优决策移动。

Input

　　第一行一个正整数n。接下来n行，每行n个整数，描述一个邻接矩阵。

Output

　　输出一行一个小数，表示最短花费时间期望。你的答案和标准答案相差的绝对值不超过10^-6时，被视为正确答案。

Sample Input

　　3
　　100 50 50
　　0 100 80
　　0 0 100

Sample Output

　　1.75000000000

HINT

　　1<=n<=1000，0<=pi,j<=100。

Solution

　　这道题有两个难点：

　　一是怎么处理反复做这件事的概率，因为道路不是100%存在，所以有极小的概率永远走不到下一个点；

　　二是怎么处理DP的顺序，概率DP的做法很显然，但这张图不是一张拓扑图（后面会讲到就算是拓扑图也不是按照拓扑序转移）。

　　曾经有一位贤者说过，“计算概率要正着算，计算期望要倒着算”。

　　姑且不论这句话的片面性，小C把这句话作为导语。

　　所以终点的期望值肯定是0，然后一步步推到起点。

　　为了解决第一个难点，首先我们考虑一下这样的情况：

　　假设现在要计算期望f的点为x，它可以到达的点为e[1]~e[cnt]，到达这些点的路出现的概率为p[1]~p[cnt]。

　　而且e[1]~e[cnt]到达终点的期望f都是已知的。

　　所以我们把e[1]~e[cnt]按照期望f从小到大排序，设排序后的数组为e'。

　　由于最小花费要求我们总是向着最优策略移动，所以当有路径通向e'[1]时，往e'[1]走肯定是最优的。

　　而通向e'[1]的路没出现时，我们就必须往e'[2]走。同理当e'[1]~e'[cnt-1]都没出现时，就必须往e'[cnt]走。

　　然而当e'[1]~e'[cnt]都没出现时，我们就必须原地等待一秒，继续重复上面的操作。

　　所以我们也就得到了求得f[x]的转移方程：

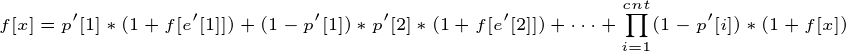
　　把1提出来，得到：

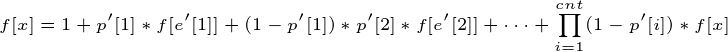
　　移项然后除过去，得：

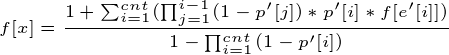
　　是不是很简单？

　　但是你可能会有疑问，为什么x是从e'[1]~e'[cnt]转移，万一f[e'[cnt]]很大怎么办？是不是只转移到e'[cnt-1]甚至更早就够了？

　　这就涉及到了第二个难点，关于转移顺序的问题。

　　我们发现这样求最短路期望其实和求最短路没有什么两样。

　　对于所有的f[x]，我们首先可以明确它是一个定值，所以每个f[x]都是从比f[x]小的期望f转移得来；

　　如果遇到比f[x]大的期望，那还不如原地等待一秒来的优呢！（其实就是从自己转移，请读者大约脑补一下）

　　所以我们可以像dijkstra那样从小到大求出最短路期望。

　　也就是每次选出当前未确定最短路期望的最小值，用这个最小值继续更新其他未确定的点。

　　这个当前选出的最小值一定就是这个点的最短路径期望，因为比它f[x]大的期望一定不会更新f[x]。

　　所以我们得出，依次求得的最短路径期望是递增的，其实这就是dijkstra算法本身的证明思路。

　　于是这两个难点都完美解决了。

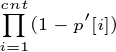　　至于如何维护信息已经很容易了，根据求f[x]的公式，我们只要维护和即可。

　　时间复杂度为dijkstra算法的O(n^2)。

#include <cstdio>

#include <cstring>

#include <algorithm>

#define MN 1005

#define INF 1LL<<62

using namespace std;

double pem[MN][MN],rem[MN],dis[MN];

double mn;

bool u[MN];

int n,mni;

inline int read()

{

    int n=,f=; char c=getchar();

    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}

    while (c>='' && c<='') {n=n*+c-''; c=getchar();}

    return n*f;

}

int main()

{

    register int i,j;

    n=read();

    for (i=;i<=n;++i)

        for (j=;j<=n;++j) pem[i][j]=(double)read()/;

    for (i=;i<=n;++i) rem[i]=,dis[i]=;

    rem[n]=dis[n]=;

    for (i=;i<=n;++i)

    {

        mn=INF;

        for (j=;j<=n;++j)

            if (!u[j]&&rem[j]<&&dis[j]/(-rem[j])<mn) mn=dis[j]/(-rem[j]),mni=j;

        dis[mni]=mn; u[mni]=true;

        if (mni==) return *printf("%.10lf",dis[mni]);

        for (j=;j<=n;++j)

            if (!u[j]) dis[j]+=rem[j]*pem[j][mni]*dis[mni],rem[j]*=(-pem[j][mni]);

    }

}

Last Word

　　这算是小C少有的一次头脑清晰地码出概率/期望DP的一道题，但小C知道丧病的题还会有多，再接再厉吧。