【uva 1411 Ants蚂蚁们】

题目大意：

·给你一个n，表示输入n个白点和n个黑点（输入每一个点的坐标）。现在需要将各个白点和各个黑点一一用线段连接起来，需要满足这些线段不能够相交。

·特色：

我们如何保证线段间不相交。

·分析：

由“黑白”可以想到用二分图匹配(最大流问题亦可)。用到一个神秘结论，可以巧妙地将“相交”和“不相交”转化为具体数值大小关系，进而转化为权值。结论为:【四边形两条对角线的和必定大于它任何一组对边的和】

用一下这幅图进行分析：

         

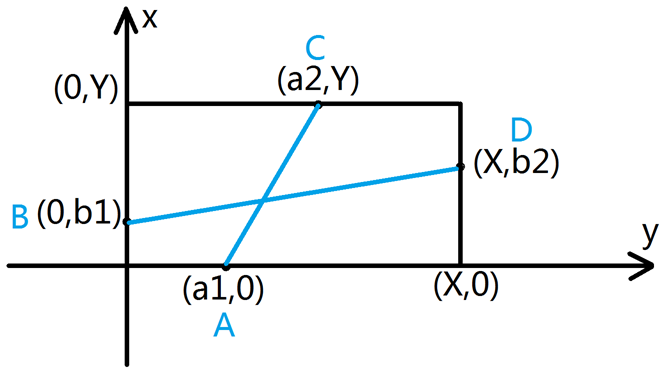
下面来比较线段交叉和不交叉情况下，两条线段和的大小：

①交叉线段:（蓝色线段）

D1=dis(A,C)+dis(B,D)

    =(a2-a1)²+Y²+(b2-b1)²+X²

②非交叉线段(这里计算AB，CD,其余情况可以用对称性等价得到)

D2=dis(A,B)+dis(C,D)

     =a1²+b1²+(X-a2)²+(Y-b2)²

【作差】：

D1-D2=dis(A,C)+dis(B,D)-dis(A,B)-dis(C,D)

           =2*b2(Y-b1)+2*a2(X-a1)

【结论】：

由于Y==b1与X==a1同时满足是不可能的(点重合了！)

又因为Y>=b1,X>=a1所以上面D1-D2的式子必为正数。

这意味着D1恒大于D2。因此这需要我们进行最小权值的二分图完全匹配。

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cmath>
 5 #define go(i,a,b) for(int i=a;i<=b;i++)
 6 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i>-1;i=e[i].next,v=e[i].v)
 7 #define mem(a,b) memset(a,b,sizeof(a))
 8 #define inf 200000000
 9 #define eps 0.000001
10 using namespace std;const int N=1003;
11 struct POS{double x,y;}white[N],black[N];
12 struct E{int v,next;double w;}e[N*N];
13 int n,head[N],k,c[N],S[N],T[N];
14 void ADD(int u,int v,double w){e[k]=(E){v,head[u],w};head[u]=k++;}
15 double A(double x){return x*x;};double slack[N],Lx[N],Ly[N];
16 double dis(POS a,POS b){return sqrt(A(a.x-b.x)+A(a.y-b.y));}
17 bool aug(int u){
18     S[u]=1;fo(i,head,u)if(!T[v])
19     {double t=Lx[u]+Ly[v]-e[i].w;if(t<eps&&t>-eps)
20     {T[v]=1;if(!c[v]||aug(c[v])){c[v]=u;return 1;}}
21     else slack[v]=min(slack[v],t);}return 0;
22 }
23 void revise(){double a=inf;
24     go(i,1,n)if(!T[i])a=min(a,slack[i]);
25     go(i,1,n)S[i]?Lx[i]-=a,1:1,T[i]?Ly[i]+=a,1:1;
26 }
27 int main(){while(~scanf("%d",&n)){
28     mem(head,-1);k=0;
29     go(i,1,n)scanf("%lf%lf",&white[i].x,&white[i].y);
30     go(i,1,n)scanf("%lf%lf",&black[i].x,&black[i].y);
31     go(i,1,n)go(j,1,n)ADD(i,j,-dis(white[i],black[j]));
32
33     go(u,1,n){Ly[u]=c[u]=0;Lx[u]=-inf;
34     fo(i,head,u)Lx[u]=max(Lx[u],e[i].w);}
35
36     go(i,1,n){go(j,1,n)slack[j]=inf;
37     for(;;){go(j,1,n)S[j]=T[j]=0;
38     if(aug(i))break;else revise();}}
39
40     go(i,1,n)go(j,1,n)if(c[j]==i)
41     {printf("%d\n",j);break;}
42 }return 0;}//Paul_Guderian

【大米饼代码】

我看见了一条河。