vlak

2023-7-14

题目

luogu题目传送门

题目描述

Nina 和 Emilija 正在玩一个特殊的游戏。这个游戏是在一张最开始为空白的纸上进行的。在每一个人的行动回合内，这个人会在这张纸上当前的单词后面加入一个字母。她们会轮流行动，而 Nina 先手行动。

操作者必须保证这样一个条件：在添加完一个字符后，整张纸上的单词必须是操作人最喜欢的歌曲的一个单词的前缀。如果不满足条件，进行这个操作的人就输了。

你的问题是，如果两个人都采取最优策略，那么谁会获得最后的胜利。

输入格式

第一行包含一个正整数 \(n\)，表示 Nina 最喜爱歌曲中的单词数量。

接下来的 \(n\) 行，每一行输入 Nina 最喜爱歌曲中的一个单词。

接下来的一行包含一个正整数 \(m\)，表示 Emilija 最喜爱歌曲中的单词数量。

接下来的 \(m\) 行，每一行输入 Emilija 最喜爱歌曲中的一个单词。

输入的单词都只包含小写字母，且单词长度总和不超过 \(200000\)。

输出格式

输出获胜的玩家，Nina 或 Emilija。

样例输入

2
aaa
bbb
3
aab
aba
bbb

样例输出

Nina

难度&重要性(1~10):5.5

题目来源

COCI，luogu

题目算法

字典树

解题思路

因为它要求必须是为喜欢的歌的前缀，那么我们就很容易想到建一个字典树记录所有歌。

在记录所有歌的同时，再用一个变量来表示这一段前缀是公共的，还是只有 Nina 或 Emilija 有。

例如样例数据：

2
aaa
bbb
3
aab
aba
bbb

建出的字典树如图:



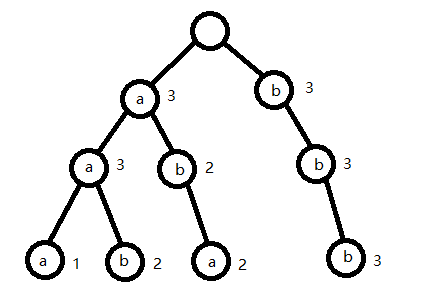
这里的 \(1\) 表示的是 Nina 的前缀，\(2\) 表示的是 Emilija 的前缀，\(3\) 表示是公共前缀。

因为是回合制的游戏，所以字典树的相邻两层是由不同的人来选择的。

我们只需要在字典树上跑一个 dfs，每一次来判断上一层的人的选择是否可行。

即如果第 \(i\) 层的第 \(j\) 个字符，如果这个人可以通过选下一层的一个字符获胜，那么就说明另一个人不应该选择第 \(i\) 层的第 \(j\) 个字符。

反之如果这个人怎么选都不可以获胜，那么就说明另一个人可以通过第 \(i\) 层的第 \(j\) 个字符获胜。

Code

void make(int k){//建字典树
	int len=s.size(),u=0;
    For(i,0,len-1){
    	int c=s[i]-'a';
        if(!ch[u][c].i)ch[u][c].i=++tot;
		if(ch[u][c].k==0)ch[u][c].k=k;//如何没有出现过，那就只有这一个人
        if(ch[u][c].k!=k)ch[u][c].k=3;//如何另一个人也有这个前缀，那这就是公共的
		u=ch[u][c].i;
    }
    return;
}

bool dfs(int u,int p){
	int k=0;
	For(i,0,25)
	if(ch[u][i].i!=0){
		if(ch[u][i].k==3)k=dfs(ch[u][i].i,!p);
		if(ch[u][i].k==1&&p==0)return 0;
		if(ch[u][i].k==2&&p==1)return 0;
		if(k)return 0;
		//如果p这个人可以获胜，即另一个人不应选u，返回0
	}
	return 1;
	//如果p这个人怎么选都获胜不了，那么另一个人就可以选u，返回1
}

signed main(){
	cin>>n;
	For(i,1,n){
        cin>>s;
        make(1);//1表示 Nina
    }

	cin>>m;
	For(i,1,m){
		cin>>s;
		make(2);//2表示 Emilija
	}

	For(i,0,25)
	if(ch[0][i].i!=0){
		ans=dfs(ch[0][i].i,1);
		//0表示 Nina
		//1表示 Emilija 

		if(ans){//如何可以获胜就输出 Nina
			cout<<"Nina";
			return 0;
		}
	}
	//如何 Nina怎么选都不能获胜，就输出 Emilija
	cout<<"Emilija";
	return 0;
}

完成状态

已完成