10-04 NOIP模拟赛

喜提80+30+10=120分

T1 水管（flow）

题目描述

某国有 $n$ 个城市，水利调配非常有问题，这导致部分地区出现严重的缺水，而部分地区却全年洪灾泛滥。政府请你来做些调整和规划。

你打算将原有的但是已经废弃了的 $m$ 条水管重新使用。第 $i$ 条水管连接城市 $x_i$ 和 $y_i$ 。

这些水管联通了所有城市。每座城市对水的需求不同设为 $a_i$，部分城市处于缺水状态，$a_i$ 为正，部分城市处于洪涝状态，$a_i$ 为负。

你需要做到每个城市都刚好满足它的需求，即缺 $a_i$ mol 水的城市需要刚好输入 $a_i$ 的水，而多出 $a_i$ mol 水的城市需要刚好输出 $a_i$ mol 水。

你需要判断能否满足要求，若满足，你还需要输出所有的 $f$

输出格式

如果不能满足要求，输出Impossible 。

如果满足要求，第一行输出Possible，接下来 $m$ 行，第 $i+1$ 行输出 $f_i$。

若有多组解，随意输出一组即可。 如果 $f_i$为0也要输出。

这道题乍一看跟网络流好像有亿点点关系，但是实则毛线关系没有。

首先一眼看出什么时候是 Impossible，即 $a_i$ 的和为 0 时才可能每个城市刚好满足他的需求，你有15了

对于满足的情况有两种方法：归一法和推流法（自己取得名字）

法一：推流法

从树根开始 dfs，你可以理解为我手中推着节点里多余的谁向前走（当然可能是负的），我走过的节点都满足需求，因为和为0，所以我走完后手上剩下的水也为0。但是这种方法略显麻烦，因为我回溯的时候也要推着水走，太不方便了。

法二：归一法

如其名，这种方法即我先遍历到叶子结点，然后回溯的时候把水全部输到根节点综合一下就行了，简单好用。

开始80分是判Impossible的时候挂了。

AC 代码：

#include<bits/stdc++.h>

using namespace std;

#define N 1200000

typedef long long LL;

int nex[N],fir[N],to[N],vis[N],ret[N],w[N],tot=0;

int n,m,dian[N>>2];

bool ward[N];

void add(int x,int y,int flag,int rt){

	nex[++tot]=fir[x];

	fir[x]=tot;

	to[tot]=y;

	ward[tot]=flag;

	ret[tot]=rt;

}

LL dfs(int u,int fa){//采用归一法

	vis[u]=1;

	int cnt=-dian[u];

	for(int e=fir[u];e;e=nex[e]){

		int v=to[e];

		if(v==fa||vis[v]) continue;

		int liu=dfs(v,u);

		cnt+=liu;

		if(ward[e]==1){

			w[ret[e]]=-liu;

		}

		else w[ret[e]]=liu;

	}

	return cnt;

}

int main(){

	freopen("flow.in","r",stdin);

	freopen("flow.out","w",stdout);

	scanf("%d",&n);

	LL sum=0;

	for(int i=1;i<=n;i++){

		scanf("%d",&dian[i]);

		sum+=dian[i];

	}

	if(sum){printf("Impossible\n");return 0;}

	scanf("%d",&m);

	for(int i=1;i<=m;i++){

		int x,y;

		scanf("%d%d",&x,&y);

		add(x,y,1,i);

		add(y,x,0,i);

	}

	printf("Possible\n");

	int hai=dfs(1,0);

	for(int i=1;i<=m;i++){

		printf("%d\n",w[i]);

	}

	return 0;

}

备注：题解也用的这种方法。

T2 宝藏（treasure）

potato 游山涉水, 想要找到埋藏在深林中的宝藏。

他偶然得到了这个深林的藏宝图, 深林可以被看作一个 $n * m$ 的矩阵。宝藏在地图中以 " $ $ $ "被标记出来，与此同时其他地方都是". "。

深林中有两条大河, 一条是纵向的, 一条是横向的。由于陆地上的宝藏都已经被人们开采完了，potato 只好转而寻求埋藏在两条大河深处的宝藏。可他并不知道大河具体在哪，也不知道大河的宽度有多少，地图上也没有标明。他唯一确定的，是两条大河横跨整个深林。

他通过小道消息得出两条大河中的宝藏的个数之和为 $\mathrm{k}$ 。请你帮 potato 统计 大河位置情况 的方案数。

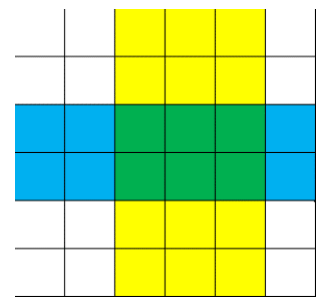
如图是两条大河的合法位置, 注意大河方向一个为横，一个为纵，且长度都是无穷大的，宽度至少为 1。蓝色和黄色分别表示了两条大河，注意它们相交的绿色区域被计算了两次贡献。

对于 $100 \%$ 的数据 $\mathrm{n}, \mathrm{t}, \mathrm{k}<=100000, \mathrm{~m}<=100$ 提示: 请注意程序的常数和空间

首先拿到这道题的时候思路是很明显的：

因为重叠部分不冲突，所以我们把行和列分开来算，考虑到m只有100，所以果断预处理每行每列的宝藏数，然后求前缀和。存在map里，然后暴力从1枚举到k，求行和列的答案数和，赛时就是这样写的，于是收货了30分。

我们只允许在时间复杂度中出现n，而不是 $n^2$。所以思考从m入手，列产生的方案最多有 $m^2$ 种，对于每一种合法的 $k'$，我们考虑使用尺取法在n中通过滑动区间的方式找出所有的 $k-k'$。

尺取法

顺便对尺取法又有了更深的理解，以往对尺取法的理解仅限于双指针模拟一个滑动区间，但是这对于目标为0的区间会出现bug，特别是一串0，而且因为有0，也会导致含有0的部分值在一个区间内值相同。

对于这种问题，先做一个前缀和，我们可以每次采用一个类似三指针的方法，即一个一个枚举右端点，然后建立两个指针，一个枚举到大于目标答案，一个枚举到大于等于目标答案，差即使答案。

for(int i=1;i<=n;i++){

         while(row[i]-row[lst-1]>K&&lst<=i)++lst;

         while(row[i]-row[j-1]>=K&&j<=i)++j;

         res+=j-lst;

      }

然后你发现其实查找过程可以用二分代替，只是多个 $log$，doge

AC 代码：

#include<bits/stdc++.h>

using namespace std;

#define N 200000

int ha[N],li[200];

int n,m,k;

long long ans=0;

map<int,int>mp1;

int main(){

	freopen("treasure.in","r",stdin);

	freopen("treasure.out","w",stdout);

	scanf("%d%d%d",&n,&m,&k);

	for(int i=1;i<=n;i++){

		char ch[200];

		scanf("%s",ch+1);

		for(int j=1;j<=m;j++){

			if(ch[j]=='$'){

				ha[i]++;

				li[j]++;

			}

		}

		ha[i]+=ha[i-1];

	}

	for(int i=2;i<=m;i++){

		li[i]+=li[i-1];

	}

	for(int len=1;len<=m;len++){

		for(int i=len;i<=m;i++){

			mp1[li[i]-li[i-len]]++;

		}

	}

	for(auto v:mp1){

		int kk=k-v.first;

		long long sum=0;

		for(int i=1;i<=n;i++){

			sum+=upper_bound(ha,ha+i,ha[i]-kk)-lower_bound(ha,ha+i,ha[i]-kk);

		}

		ans+=sum*v.second;

	}

	printf("%lld",ans);

	return 0;

}

顺便学习了map的遍历，大大的好！