玩转OpenHarmony PID：教你打造两轮平衡车

简介

此次为大家带来的是OpenAtom OpenHarmony（以下简称“OpenHarmony”）系统与PID控制算法相结合并落地的平衡车项目。

PID控制算法是一种经典的，并被广泛应用在控制领域的算法。类似于这种：需要将某一个物理量保持稳定的场合，比如维持平衡，稳定温度、转速等，PID都会适用。在四轴飞行器，平衡小车、汽车定速巡航、温度控制器等场景均有应用。

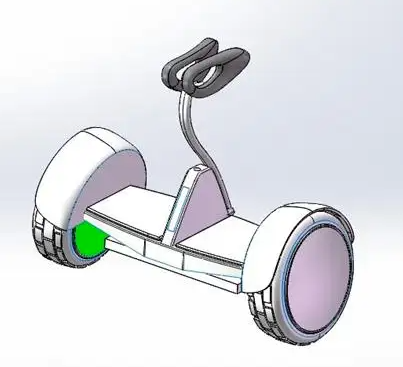
通过本样例的学习，开发者能够对OpenHarmony系统设备端开发有进一步的认识，还能够掌握PID控制算法的使用。本样例使用OpenHarmony 3.2 Beta1操作系统，硬件平台采用小熊派BearPi-HM Nano（Hi3861）开发板。

本样例效果动图：

硬件配置资源

两轮平衡小车主要硬件资源：

主控CPU：小熊派BearPi-HM Nano（Hi3861）开发板；

陀螺仪：MPU6050六轴陀螺仪传感器；

左右轮：带有霍尔传感器的直流电机；

小车平台及结构件资源可以自行在相关网站获得。

原理概括

小时候都玩过上图游戏吧：木杆立在手指上，尽量保持木杆直立不倒。

当木杆向前倾斜时，我们会往前行走，以用来抵消木杆的前倾；往后倾斜时，我们会往后倒退。对的！没错！你猜对了。平衡车的控制原理就是这样：

PID算法介绍

平衡车的控制离不开对PID算法的应用。那么什么是PID算法？它能解决什么问题？

PID算法：就是“比例（proportional）、积分（integral）、微分（derivative）”，是一种常见的“保持稳定”控制算法。

结合两轮平衡车的场景，对PID参数的认识如下：

P比例参数：该参数能够快速让小车达到平衡状态，但是由于控制是滞后的，以及是惯性系统，容易带来超调，即小车会出现前后摇摆的现象。所以P参数不能太大；

I积分参数：小车由于摩擦力或者风阻力，并且P不能太大，只靠P控制有可能达不到稳定状态，所以需要加入I积分参数，消除稳态误差；

D微分参数：平衡小车维持的是倾斜角度要为平衡角度，由于PI参数使小车振荡，小车会出现前后摇摆现象，加入D微分参数能够消除小车的振荡。

两步搭建样例工程

在OpenHarmony源码基础上，两步构建平衡小车代码。（OpenHarmony源码下载路径及BearPi-HM Nano（Hi3861）开发板代码烧录，请参考文章末尾相关链接）

第一步：拷贝Balance_car文件夹到源码路径下：\device\board\bearpi\bearpi_hm_nano\app\ （Balance_car文件获取路径，请参考文章末尾相关链接）

如图文件夹目录：

第二步：修改BUILD.gn，在源码路径下：\device\board\bearpi\bearpi_hm_nano\app\BUILD.gn

添加编译依赖："Balance_car:balance_car"，如下图：

关键算法讲解

两轮平衡车的控制主要涉及三个PID环的串联使用，它们分别是直立环（平衡控制）、速度环（速度控制）、转向环（方向控制）。三个控制效果合成，控制轮子运行。

直立环控制算法：

直立环控制算法是平衡小车维持平衡的主要算法。直立环采用了PD算法环节，即只有比例与微分环节。

倾斜角度大小以及角加速度大小决定了轮子的速度大小。可以理解为倾斜角度越大，控制轮子顺着倾斜的方向的速度越大；倾斜的角加速度越大，控制轮子速度也要越大。

float g_middleAngle = 1.0;//平衡角度

float g_kpBalance = -85800.0;

float g_kdBalance = -400;

static int ControlBalance(float angle, short gyro)

{

    int outpwm = 0;

    float angleBias = 0.0;

    float gyroBias = 0.0;

    float tempAngle = 0.0;

    float tempGyro = 0.0;

    tempAngle = 0 - angle;//极性控制

    tempGyro = 0 - gyro;

    angleBias = g_middleAngle - tempAngle;

    gyroBias = 0 - tempGyro;

    outpwm = (g_kpBalance / 100 * angleBias + g_kdBalance

     * gyroBias / 100);

    return outpwm;

}

速度环控制算法：

速度环控制的目的是让机器以恒定速度前进或后退，该恒定速度可以为0速度，即要让平衡车静止。速度环采用了PI环控制，只有比例与积分环节。

float g_kpSpeed = 95800.0;

float g_kiSpeed = 200;

static int ControlSpeed(long int left, long int right)

{

    int outpwm = 0;

    int speedBias = 0;

    int speedBiasLowpass = 0;

    static int speed_i = 0;

    float a = 0.68;

    static int speedBiasLast = 0;

    speedBias = 0 - left - right;

    speedBiasLowpass = (1 - a) * speedBias

        + a * speedBiasLast;

    speedBiasLast = speedBiasLowpass;

    speed_i += speedBiasLowpass;

    speed_i = limit_data(speed_i, SPEED_H, SPEED_L);

    outpwm = (g_kpSpeed * speedBiasLowpass / 100 +

        gkiSpeed * speed_i / 100);

    return outpwm;

}

转向环控制算法：

转向环的目的是控制小车以恒定速度转向。在本次场景为了控制小车平衡静止，所以只做了限制转向的操作。

static int ControlTurn(short gyro)

{

  int outpwm;

    outpwm = g_kpTurn * gyro;

  return outpwm;

}

以上详细代码，请参考文章末尾的相关链接（Balance_car文件获取路径）。

总结

本文呈现了两轮平衡小车的大致原理。简单介绍了一下PID算法的效果：P比例参数，能够快速让系统达到稳定值，但是P太大容易超调，带来振荡；I积分参数，消除稳态误差，让系统达到稳定值；D积分参数，能消除振荡，但是会使系统时效性变慢。开发者可以根据现场情况，合理调节PID三个参数。

本样例是OpenHarmony知识体系工作组（相关链接在文章末尾）为广大开发者分享的样例。同时知识体系工作组结合日常生活，给开发者规划了各种场景的Demo样例，如智能家居场景、影音娱乐场景、运动健康场景等；欢迎广大开发者一同参与OpenHarmony的开发，更加完善样例，相互学习，相互进步。