普及模拟2 +【LGR-155-Div.3】洛谷基础赛 #3 &「NnOI」Round 2

普及模拟2

\(T1\) 地址 \(0pts\)

• 简化题意：判断一个 \(IP\) 地址是否合法（数据保证字符串中存在且仅存在4个被字符分开的整数），若不合法则将其改正。
• 部分分：
  • \(0pts\) ：输出 Yes ，不,可以，总司令。
    • 然鹅根本就没有输出合法的数据点
• 正解：

  char s[100];
  int main()
  {
  	freopen("ip.in","r",stdin);
  	freopen("ip.out","w",stdout);
  	int len,i,sum=0,x=0,num=0,flag=0;
  	cin>>(s+1);
  	len=strlen(s+1);
  	s[len+1]='.';//赛时写成s[i+1]='.'了，挂了100pts
  	len++;
  	for(i=1;i<=len;i++)
  	{
  		if('0'<=s[i]&&s[i]<='9')
  		{
  			if(!('0'<=s[i-1]&&s[i-1]<='9'))
  			{
  				if('0'<=s[i+1]&&s[i+1]<='9')
  				{
  					if(s[i]=='0')
  					{
  						flag=1;
  						break;
  					}
  				}
  			}
  			x=x*10+s[i]-'0';
  		}
  		else
  		{
  			if(x>255||s[i]!='.')
  			{
  				flag=1;
  				break;
  			}
  			if(s[i]=='.')
  			{
  				num++;
  			}
  			if(num>=4)
  			{
  				flag=1;
  				break;
  			}
  			x=0;
  		}
  	}
  	if(flag==0&&num==3)
  	{
  		cout<<"YES"<<endl;
  	}
  	else
  	{
  		x=flag=0;
  		cout<<"NO"<<endl;
  		for(i=1;i<=len;i++)
  		{
  			if('0'<=s[i]&&s[i]<='9')
  			{
  				x=x*10+s[i]-'0';
  				flag=1;
  			}
  			else
  			{
  				if(flag==1)
  				{
  					sum++;
  					if(sum<=4)
  					{
  						cout<<min(x,255);
  					}
  					if(sum<=3)
  					{
  						cout<<".";
  					}
  					if(sum==4)
  					{
  						break;
  					}
  				}
  				x=flag=0;
  			}
  		}
  	}
  	return 0;
  }
  

\(T2\) 内积 \(100pts\)

• 原题：SP1025 FASHION - Fashion Shows
• 考虑将数组 \(a,b\) 排序，此时的 \(\sum\limits_{i=1}^{n}=a_i b_i\) 即为所求。
  • 前置知识：若 \(a_1<a_2,b_1<b_2\) ，有 \(a_1 b_1+a_2 b_2>a_1 b_2+a_2 b_1\) 。
    • 证明：因为 \(a_1<a_2,b_1<b_2\) ，所以有 \(b_2-b_1>0,a_2-a_1>0\) ，故 \((a_2-a_1) (b_2-b_1)>0\) ，展开得 \(a_2 b_2-a_2 b_1-a_1 b_2+a_1 b_1>0\) ，移项得 \(a_1 b_1+a_2 b_2>a_1 b_2+a_2 b_1\) 。

  #define ll __int128_t //赛时怕炸long long就开了int128，但不开int128也能过
  ll read()
  {
  	ll x=0,f=1;
  	char c=getchar();
  	while(c>'9'||c<'0')
  	{
  		if(c=='-')
  		{
  			f=-1;
  		}
  		c=getchar();
  	}
  	while('0'<=c&&c<='9')
  	{
  		x=x*10+c-'0';
  		c=getchar();
  	}
  	return x*f;
  }
  void write(ll x)
  {
  	if(x<0)
  	{
  		putchar('-');
  		x=-x;
  	}
  	if(x>9)
  	{
  		write(x/10);
  	}
  	putchar((x%10)+'0');
  }
  ll a[2000001],b[2000001];
  int main()
  {
  	freopen("nj.in","r",stdin);
  	freopen("nj.out","w",stdout);
  	ll n,i,ans=0;
  	n=read();
  	for(i=1;i<=n;i++)
  	{
  		a[i]=read();
  	}
  	for(i=1;i<=n;i++)
  	{
  		b[i]=read();
  	}
  	sort(a+1,a+1+n);
  	sort(b+1,b+1+n);
  	for(i=1;i<=n;i++)
  	{
  		ans+=a[i]*b[i];
  	}
  	write(ans);
  	return 0;
  }
  

\(T3\) 翻转 \(10pts\)

• 原题：luogu P1764 翻转游戏 (加强版)
• 弱化版：luogu P2040 打开所有的灯
• 部分分：
  • \(0pts\) ：不可以，总司令。
    • 然鹅根本就没有输出无解的数据点
  • \(10pts\) ：输出 0 。
• 正解：
  • 观察到 \(1 \le n \le 16\) ，考虑爆搜。开两个数组 \(a,b\) 分别记录最终结果都为白色或都为黑色是否需要翻转（若值为 \(1\) 则需要翻转，值为 \(0\) 则不需要翻转）。考虑从左到右进行搜索，搜到第 \(n+1\) 列时切换到下一行，当搜到第 \(n+1\) 行判断当前状态是否可行。
    • 当搜索到第 \(i\) 行，第 \(j\) 列的点时，只需要考虑第 \(i-1\) 行，第 \(j\) 列的点状态是否可行。因为对第 \(i\) 行，第 \(j\) 列进行翻转，对第 \(i-1\) 行产生影响的点仅有第 \(i-1\) 行，第 \(j\) 列的点，而且后续搜索时也不会影响到第 \(i-1\) 行，第 \(j\) 列的点。

  int a[20][20],b[20][20],vis1[20][20],vis2[20][20],ans=0x7f7f7f7f;
  int check1(int x,int y)
  {
  	if(x==0||y==0)
  	{
  		return 0;
  	}
  	else
  	{
  		return (a[x][y]+vis1[x][y]+vis1[x-1][y]+vis1[x+1][y]+vis1[x][y-1]+vis1[x][y+1])%2;//(x,y)受到(x-1,y),(x+1,y),(x,y-1),(x,y+1)的影响，两次翻转会相互抵消所以模2
  	}
  }
  int check2(int x,int y)
  {
  	if(x==0||y==0)
  	{
  		return 0;
  	}
  	else
  	{
  		return (b[x][y]+vis2[x][y]+vis2[x-1][y]+vis2[x+1][y]+vis2[x][y-1]+vis2[x][y+1])%2;
  	}
  }
  void dfs1(int x,int y,int num,int n)//num为翻转次数
  {
  	if(num>=ans)//剪枝：如果当前操作次数大于或等于答案时直接return
  	{
  		return;
  	}
  	if(y==n+1)//当搜到第n+1列时，切换到下一行
  	{
  		x++;
  		y=1;
  	}
  	if(x==n+1)
  	{
  		for(int i=1;i<=n;i++)//判断当前状态
  		{
  			if(check1(n,i)==1)
  			{
  				return;//说明当前状态不合法
  			}
  		}
  		ans=min(ans,num);//进行转移
  		return;
  	}
  	vis1[x][y]=0;//将(x,y)不进行翻转
  	if(check1(x-1,y)==0)
  	{
  		dfs1(x,y+1,num,n);
  	}
  	vis1[x][y]=1;//将(x,y)进行翻转
  	if(check1(x-1,y)==0)
  	{
  		dfs1(x,y+1,num+1,n);
  	}
  }
  void dfs2(int x,int y,int num,int n)
  {
  	if(num>=ans)
  	{
  		return;
  	}
  	if(y==n+1)
  	{
  		x++;
  		y=1;
  	}
  	if(x==n+1)
  	{
  		for(int i=1;i<=n;i++)
  		{
  			if(check2(n,i)==1)
  			{
  				return;
  			}
  		}
  		ans=min(ans,num);
  		return;
  	}
  	vis2[x][y]=0;
  	if(check2(x-1,y)==0)
  	{
  		dfs2(x,y+1,num,n);
  	}
  	vis2[x][y]=1;
  	if(check2(x-1,y)==0)
  	{
  		dfs2(x,y+1,num+1,n);
  	}
  }
  int main()
  {
  	freopen("fz.in","r",stdin);
  	freopen("fz.out","w",stdout);
  	int n,i,j;
  	char pd;
  	cin>>n;
  	for(i=1;i<=n;i++)
  	{
  		for(j=1;j<=n;j++)
  		{
  			cin>>pd;
  			if(pd=='b')
  			{
  				a[i][j]=1;
  				b[i][j]=0;
  			}
  			else
  			{
  				a[i][j]=0;
  				b[i][j]=1;
  			}
  		}
  	}
  	dfs1(1,1,0,n);
  	dfs2(1,1,0,n);
  	if(ans==0x7f7f7f7f)
  	{
  		cout<<"Impossible"<<endl;
  	}
  	else
  	{
  		cout<<ans<<endl;
  	}
  	return 0;
  }
  

\(T4\) 阶乘 \(40pts\)

• 简化题意： \(T\) 组询问，每组询问给出 \(n\) ，求出所有满足 \(n=\dfrac{a!}{b!}\) 的 \(a,b\) 及数量或给出无解信息（输出 -1 ）。

• 赛时乱搞的一个算法：预处理 \(1 \sim 30\) 的阶乘，然后枚举右端点一直到 \(30\) ，接着枚举左端点，骗到了 \(40pts\) 。

• 正解：

  • \(n=1\) 时，输出 -1 。
  • \(n \in \mathbb{P}\) 时，仅存在一组答案 \(a=n,b=n-1\) 。
  • 打表发现阶乘的增长速度极快，\(20! \approx 2 \times 10^{18}\) ，发现有 \(a-b \le 20\) ，枚举 \(d=a-b\) ，那么一定有 \(a^d \le n,b^d \ge n\) ，即 \(a \le \sqrt[d]{n},b \ge \sqrt[d]{n}\) （设 \(a(a+1)(a+2)(a+3)(a+4)=n\) ，有 \(a,a+1,a+2,a+3,a+4\) 均在 \(\sqrt[5]{n}\) 附近）。

  priority_queue<pair<ll,ll> >q;
  int main()
  {
  	freopen("jc.in","r",stdin);
  	freopen("jc.out","w",stdout);
  	ll t,n,i,l,r,len,j,sum,ls;
  	scanf("%lld",&t);
  	for(i=1;i<=t;i++)
  	{
  		scanf("%lld",&n);
  		if(n==1)
  		{
  			printf("-1\n");
  		}
  		else
  		{
  			sum=0;
  			for(len=2;len<=20;len++)//如果枚举到20不放心，可以再大一点
  			{
  				for(r=pow(1.0*n,1.0/len);;r++)
  				{
  					l=r-len+1;
  					if(l!=1)//特判l=1的时候 ，此时有b=0，但是除数不能为0
  					{
  						ls=1;
  						for(j=l;j<=r;j++)//直接枚举阶乘就行，也可以事先预处理出阶乘
  						{
  							ls*=j;
  						}
  						if(ls>n)
  						{
  							break;
  						}
  						if(ls==n)
  						{
  							sum++;
  							q.push(make_pair(-r,-(l-1)));
  							break;
  						}
  					}
  				}
  			}
  			sum++;
  			q.push(make_pair(-n,-(n-1)));//因为枚举长度大于1，所以会漏掉a=n,b=n-1的情况
  			printf("%lld\n",sum);
  			for(j=1;j<=sum;j++)
  			{
  				printf("%lld %lld\n",-q.top().first,-q.top().second);
  				q.pop();
  			}
  		}
  	}
  	return 0;
  }
  

【LGR-155-Div.3】洛谷基础赛 #3 &「NnOI」Round 2

这场比赛和上午模拟赛讲评时间重了，打完 \(T1,T2\) 就溜了。

\(T1\) luogu P9569 Khronostasis Katharsis \(100pts\)

• 水题

  int main()
  {
      ll n,m,i,v,t,ans=0,l=1;//l要初始化为1（当T=1时），赛时在这里卡了10min
      cin>>n>>m;
      for(i=1;i<=n;i++)
      {
          cin>>v>>t;
          if((m-t)*v>ans)
          {
              ans=(m-t)*v;
              l=i;
          }
      }
      cout<<l;
      return 0;
  }
  

\(T2\) luogu P9570 Glaciaxion \(100pts\)

• 水题

  char s[1000001];
  int main()
  {
  	int n,m,i,flag=0,sumn=0,l=0,r=0;
  	char pd;
  	cin>>n>>m>>(s+1);
  	for(i=1;i<=m;i++)
  	{
  		if(s[i]=='N')
  		{
  			sumn++;
  		}
  		if(s[i]=='Y'&&sumn==0)
  		{
  			cout<<"No solution"<<endl;
  			flag=1;
  			break;
  		}
  	}
  	if(flag==0)
  	{
  		if(sumn>n)
  		{
  			cout<<"No solution"<<endl;
  		}
  		else
  		{
  			for(i=1;i<=m;i++)
  			{
  				if(s[i]=='N')
  				{
  					l++;
  					cout<<l<<" ";
  				}
  				if(s[i]=='Y')
  				{
  					cout<<"1 ";
  				}
  			}
  		}
  	}
  	return 0;
  }
  

\(T3\) luogu P9571 Horizon Blue \(0pts\)

• 前置知识：两条直线只要 \(k\) 不同，这两条直线就会相交且只有一个公共点。
• \(map\) 大法好，开一个 \(map\) 记录 \(y=kx+b\) 的直线个数。令 \(len[i]\) 表示斜率为 \(i\) 的直线个数。
• 其他细节：考虑到 \(1 \le |k| \le 10^5\) ，事先给 \(k\) 加上一个大点的常数（eg： \(1000000\) ），防止出现负数。

  int k[3000000],b[3000000],len[3000000];
  map<pair<int,int>,int>a;
  int main()
  {
  	int n,i,j,pd,ans=0,x,y,m=0,sum=0,ls;//sum用来存储当前画板上直线的条数
  	cin>>n;
  	for(i=1;i<=n;i++)
  	{
  		cin>>pd>>x>>y;
  		x+=1000000;//防止出现负数
  		if(pd==1)
  		{
  			if(a[make_pair(x,y)]==0)
  			{
  				m++;
  				k[m]=x;
  				b[m]=y;
  			}
  			a[make_pair(x,y)]++;
  			len[x]++;
  			sum++;
  		}
  		if(pd==2)
  		{
  			cout<<sum-len[x]<<endl;//当前画板上直线的条数减去斜率为x的直线的条数即为答案
  		}
  		if(pd==3)
  		{
  			ls=m;
  			m=0;
  			for(j=1;j<=ls;j++)
  			{
  				if(k[j]!=x)//若当前画板上直线的斜率不为x，就将其抹去
  				{
  					len[k[j]]=0;
  					a[make_pair(k[j],b[j])]=0;
  				}
  				else//斜率为x的存回原数组
  				{
  					m++;
  					k[m]=k[j];
  					b[m]=b[j];
  				}
  			}
  			sum=len[x]-a[make_pair(x,y)];//抹去重合的直线
  			len[x]-=a[make_pair(x,y)];//抹去重合的直线
  			a[make_pair(x,y)]=0;//抹去重合的直线
  		}
  	}
  	return 0;
  }
  

\(T4\) luogu P9572 Colorful Days♪ \(0pts\)

• 暂时咕了，有时间再打。

总结

• 上午模拟赛打到 \(8:50\) 就溜去打别的东西了，导致 \(T1\) 没有造出合理的 \(hack\) 数据，挂了 \(100pts\) 。

后记

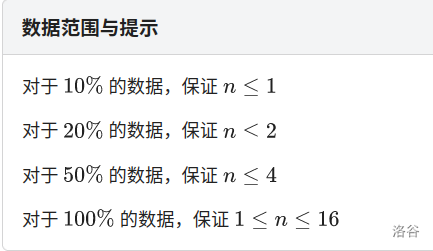
• 众所周知，上午的 \(T3\) 有 \(4\) 个数据范围。