机器学习实战笔记(Python实现)-04-Logistic回归

---------------------------------------------------------------------------------------

本系列文章为《机器学习实战》学习笔记，内容整理自书本，网络以及自己的理解，如有错误欢迎指正。

源码在Python3.5上测试均通过，代码及数据 --> https://github.com/Wellat/MLaction

---------------------------------------------------------------------------------------

1、算法概述

利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“ 回归” 一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。

在做分类时，我们总是希望分类函数能够接受所有输入然后预测出类别。以两类为例，分类函数输出0或1，我们知道单位阶跃函数满足这种性质。然而，在跳跃点上从0瞬间到1，这个过程有时很难处理，幸好，Sigmoid函数有类似的性质，在数学上更易处理。Sigmoid函数公式如下：

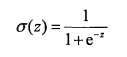
像阶跃函数的Sigmoid的效果图是这样的：

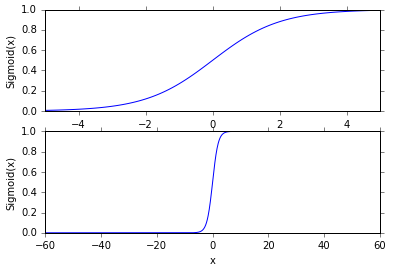
为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类 ，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

那么问题来了，这个回归系数要如何确定？且往下看。

2、基于最优化方法的最佳回归系数确定

设输入数据x有n个特征，即n维，由以上知Sigmoid函数的输入z可表示为：

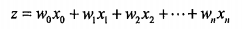
采用向量的写法，上式可以写成 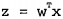 ，向量w就是我们要找的最佳系数。

2.1 梯度上升法

基本思想：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。

如果梯度记为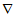，则函数 f(x,y) 的梯度表示为：

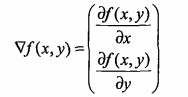
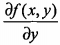这个梯度意味着要沿x的方向移动，沿y的方向移动。可以看到梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记做α。用向量来表示的话，梯度算法的迭代公式如下：

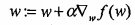
该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

基于上面的内容，我们来看Python的实现。

 from numpy import *
 
 def loadDataSet():
     dataMat = []; labelMat = []
     fr = open('testSet.txt')
     for line in fr.readlines():
         lineArr = line.strip().split()
         #为方便计算将x0设为1.0
         dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
         labelMat.append(int(lineArr[2]))
     return dataMat,labelMat
 
 def sigmoid(inX):
     return 1.0/(1+exp(-inX))
 
 def gradAscent(dataMatIn, classLabels):
     '''
     梯度上升算法
     dataMatIn:2维NumPy数组 (100x3)
     classLabels:类标签 (1x100)
     '''
     #将输入转换为NumPy矩阵的数据类型
     dataMatrix = mat(dataMatIn)
     labelMat = mat(classLabels).transpose()
     m,n = shape(dataMatrix)
     #向目标移动的步长
     alpha = 0.001
     #迭代次数
     maxCycles = 500
     weights = ones((n,1))
     for k in range(maxCycles):
         h = sigmoid(dataMatrix*weights)
         error = (labelMat - h)
         weights = weights + alpha * dataMatrix.transpose()* error
     return weights

2.2 绘制决策边界图

上节解出了一组回归系数，它确定了不同类别数据之间的分隔线，接下来画出这条线。

 def plotBestFit(dataMat,labelMat,weights):
     '''
     画出数据集和Logistic回归最佳拟合直线的函数
     '''
     import matplotlib.pyplot as plt
     dataArr = array(dataMat)
     n = shape(dataArr)[0]
     xcord1 = []; ycord1 = []
     xcord2 = []; ycord2 = []
     #根据类别分别保存点
     for i in range(n):
         if int(labelMat[i])== 1:
             xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
         else:
             xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
     fig = plt.figure()
     ax = fig.add_subplot(111)
     ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
     ax.scatter(xcord2, ycord2, s=30, c='green')
     x = arange(-3.0, 3.0, 0.1)
     #此处设置了Sigmoid的z为0，因为0是两个分类的分界处
     #即：0=w0x0+w1x1+w2x2
     #注意：x0=1,x1=x,解出x2=y
     y = (-weights[0]-weights[1]*x)/weights[2]
     ax.plot(x, y.transpose())
     plt.xlabel('X1'); plt.ylabel('X2');
     plt.show()

结果：

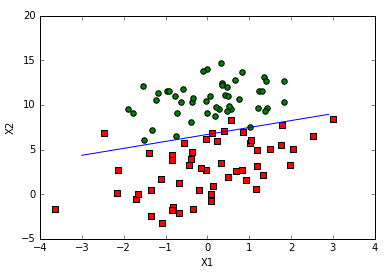
2.3 随机梯度上升法

梯度上升算法在每次更新回归系数时都需要遍历整个数据集，当数据量庞大时，那么此方法计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。

 def stocGradAscent1(dataMatrix, classLabels, numIter=500):
     '''
     改进的随机梯度算法
     '''
     dataMatrix = array(dataMatrix)
     m,n = shape(dataMatrix)
     weights = ones(n)
     for j in range(numIter):
         dataIndex = list(range(m))
         for i in range(m):
             #alpha会随着迭代次数不断减小，但存在常数项，它不会小到0
             #这种设置可以缓解数据波动
             alpha = 4/(1.0+j+i)+0.0001
             #通过随机选取样本来更新回归系数
             randIndex = int(random.uniform(0,len(dataIndex)))
             h = sigmoid(sum(dataMatrix[randIndex]*weights))
             error = classLabels[randIndex] - h
             weights = weights + alpha * error * dataMatrix[randIndex]
             del(dataIndex[randIndex])
     return weights

改进的随机梯度算法得到了与GrdientAscent()差不多的分类效果，但是计算复杂度大幅降低。

3、实例：从疝气病症预测病马的死亡率

数据包括368个样本和28个特征，数据集中有30%的值缺失。下面首先介绍如何处理缺失值，之后利用Logistic回归和随机梯度上升算法预测病马的生死。

3.1 处理数据中的缺失值

常用处理缺失值的做法：

• 使用可用特征的均值来填补缺失值；
• 使用特殊值来填补缺失值，如-1；
• 忽略有缺失值的样本；
• 使用相似样本的均值添补缺失值；
• 使用另外的机器学习算法预测缺失值

本例中用0来填充缺失值，因为某特征对应值为0，那么它对系数更新不会产生影响，另外，sigmoid(0)=0.5，它对结果的预测不具有任何倾向性。

若测试数据集中数据的类标签缺失，则丢弃该条数据。

3.2 用Logistic回归进行分类

本例直接使用已预处理的数据，对应horseColicTest.txt和horseColicTraining.txt。

 def colicTest():
     frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
     trainingSet = []; trainingLabels = []
     for line in frTrain.readlines():
         currLine = line.strip().split('\t')
         lineArr =[]
         for i in range(21):
             lineArr.append(float(currLine[i]))
         trainingSet.append(lineArr)
         trainingLabels.append(float(currLine[21]))
     trainWeights = stocGradAscent1(trainingSet, trainingLabels, 1000)
     errorCount = 0; numTestVec = 0.0
     for line in frTest.readlines():
         numTestVec += 1.0
         currLine = line.strip().split('\t')
         lineArr =[]
         for i in range(21):
             lineArr.append(float(currLine[i]))
         if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
             errorCount += 1
     errorRate = (float(errorCount)/numTestVec)
     print("the error rate of this test is: %f" % errorRate)
     return errorRate
 
 def multiTest():
     '''
     多次调用colicTest()函数，求结果的平均值
     '''
     numTests = 10; errorSum=0.0
     for k in range(numTests):
         errorSum += colicTest()
     print("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))
 
 def classifyVector(inX, weights):
     '''
     分类函数
     '''
     prob = sigmoid(sum(inX*weights))
     if prob > 0.5: return 1.0
     else: return 0.0

THE END.