TDOA 基础之 双曲线
TDOA 的算法基础就是时间差,根据时间差换算出距离差,后面的数学理论知识就是双曲线交点问题。
双曲线方程是2次方程,解算曲线交点也就是两个2次方程求解。
首先看双曲线定义(百度百科):
双曲线(Hyperbola)是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹 [1] 。双曲线是圆锥曲线的一种,即圆锥面与平行于中轴的平面的交截线。

而我们实际放置基站的时候,不是原点对称的,但是我们可以根据对称点对x y进行移位产生新的双曲线方程
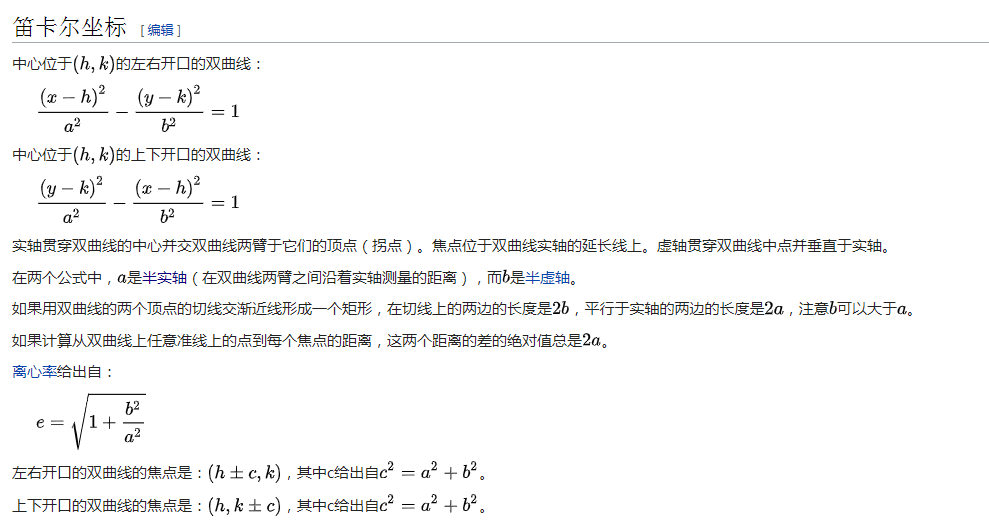
其中(h,k)就是放置基站中心对称点,双曲线焦点是基站坐标点。
对于放置好的两个基站可以知道h k 以及c,通过发送电磁信号可以求得距离差a,对于一个给定点的双曲线方程就可以简化成一个2元2次方程 Ax2+By2=1
同理在增加一个基站,又会多出两个双曲线方程,利用其中一个方程,可以得到 Cx2+Dy2=1
联立两个方程即可求出x y
此时此时x y 可能有4个坐标,我们可以假定我们的标签只能在第一象限活动,限制条件为x>0 and y>0最终获得标签坐标
更多内容参考蓝点无限论坛bphero.com.cn
TDOA 基础之 双曲线的更多相关文章
- TDOA基础之 delayed tx 实现说明
不论是在TWR 还是TDOA定位算法中,delayed tx 都会用到,这篇博文主要解析delayed tx 实现. 何为delayed tx? delayed tx 是延时发送,为何要延时?因为这个 ...
- Deep Learning基础--26种神经网络激活函数可视化
在神经网络中,激活函数决定来自给定输入集的节点的输出,其中非线性激活函数允许网络复制复杂的非线性行为.正如绝大多数神经网络借助某种形式的梯度下降进行优化,激活函数需要是可微分(或者至少是几乎完全可微分 ...
- HLSL Shader编程基础总结
转自:https://blog.csdn.net/Blues1021/article/details/47093487 基本前提概念 Shader是一种映射到GPU硬件汇编语言上的高级语言,Shade ...
- TDOA 之TDOA算法python实现
这里指的TDOA算法,实际是解两个双曲线方程,由于两个二次方程设计东西较多,如果强解,计算量很大,从网上参考了如下链接: 算法推到:https://blog.csdn.net/lpsl1882/art ...
- TDOA基站 之 时间同步
TDOA 和 TWR相比,标签可以用最少的信息来定位,但是对于基站要求很高,需要“时间同步”. 这也是TDOA算法的核心部分,很多套件对此讳莫如深,希望能沟通过本文使读者能对TODA同步有一定初步了解 ...
- java基础集合经典训练题
第一题:要求产生10个随机的字符串,每一个字符串互相不重复,每一个字符串中组成的字符(a-zA-Z0-9)也不相同,每个字符串长度为10; 分析:*1.看到这个题目,或许你脑海中会想到很多方法,比如判 ...
- node-webkit 环境搭建与基础demo
首先去github上面下载(地址),具体更具自己的系统,我的是windows,这里只给出windows的做法 下载windows x64版本 下载之后解压,得到以下东西 为了方便,我们直接在这个目录中 ...
- js学习笔记:webpack基础入门(一)
之前听说过webpack,今天想正式的接触一下,先跟着webpack的官方用户指南走: 在这里有: 如何安装webpack 如何使用webpack 如何使用loader 如何使用webpack的开发者 ...
- Golang, 以17个简短代码片段,切底弄懂 channel 基础
(原创出处为本博客:http://www.cnblogs.com/linguanh/) 前序: 因为打算自己搞个基于Golang的IM服务器,所以复习了下之前一直没怎么使用的协程.管道等高并发编程知识 ...
随机推荐
- [C#] - 从 HTML 代码中 转换 / 提取 可读文字(PlainText)的方法
背景 在做网页数据分析的时候,我们关注的部分是内容,可以过滤掉HTML标签.Javascript.CSS等代码. 目标输入 <b>Hello World.</b><br/ ...
- 多线程(7)— JDK对锁优化的努力
JDK内部的“锁”优化策略 1. 锁偏向 锁偏向是针对加锁操作的优化手段,核心思想是:如果一个线程获得了锁,那么锁就进入偏向模式,当这个线程再次请求锁时,无须再做任何同步操作,这样就节省了大量有关锁申 ...
- WUSTOJ 1318: 区间的连通性(Java)
题目链接:
- FFmpeg开发教程一、FFmpeg 版 Hello world
本系列根据项目ffmpeg-libav-tutorial翻译而来 Chapter 0 - 万物之源 -- hello world 然而,本节的程序并不会在终端打印"Hello world&q ...
- (未完成)ARM-linux 移植 SDL
ref : https://blog.csdn.net/u012075739/article/details/24877639 2. 交叉编译SDL 编译SDL前先要编译其依赖库 tsl ...
- [Luogu5280][ZJOI2019]线段树(线段树+DP)
https://www.luogu.org/blog/Sooke/solution-p5280 首先想到对线段树上每个点分别维护有多少棵线段树在它上有标记(f[]),然后想到对于每个操作,根据转移的不 ...
- [NOIP11.1模拟赛]补番报告
Preface 昨天开始补某科学的超电磁炮S 感觉今天就好了点,炮姐赛高 T1 一开始一直想欧拉定理&ex欧拉定理,结果估计70分,数组开小了GG,看了正解发现是我学傻了 T2 一看就是数据结 ...
- MonkeyRunner——Mac
1. MonkeyRunner介绍: Android的SDK中集成了三个可用来进行自动化测试的工具:Monkey.MonkeyRunner和Robotium.这三个测试工具都是基于黑盒测试. Monk ...
- OpenStack kilo版(5) Neutron部署
neutron简介: Neutron 通过 plugin 和 agent 提供的网络服务. plugin 位于 Neutron server,包括 core plugin 和 service plug ...
- JetBrains 系列开发工具 汉化(中文化)教程
项目地址:(* ̄3 ̄)╭ 操作流程: 拷贝内容 将下载的包改名为resources_cn.jar,拷贝到 $IDEA_HOME$/lib/ 目录下 重启IDEA 打开或者重新启动IDEA
