poj1178 floyd+枚举

http://poj.org/problem?id=1178

Description

Centuries ago, King Arthur and the Knights of the Round Table used to meet every year on New Year's Day to celebrate their fellowship. In remembrance of these events, we consider a board game for one player, on which one king and several knight pieces are placed
at random on distinct squares. 

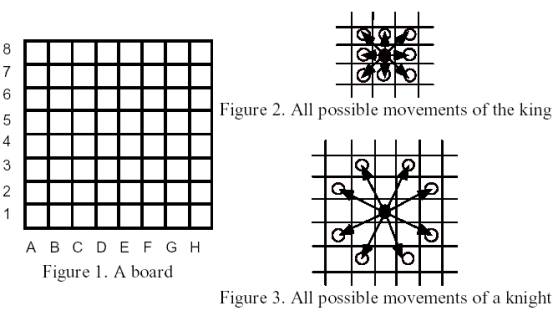
The Board is an 8x8 array of squares. The King can move to any adjacent square, as shown in Figure 2, as long as it does not fall off the board. A Knight can jump as shown in Figure 3, as long as it does not fall off the board. 




During the play, the player can place more than one piece in the same square. The board squares are assumed big enough so that a piece is never an obstacle for other piece to move freely. 

The player's goal is to move the pieces so as to gather them all in the same square, in the smallest possible number of moves. To achieve this, he must move the pieces as prescribed above. Additionally, whenever the king and one or more knights are placed in
the same square, the player may choose to move the king and one of the knights together henceforth, as a single knight, up to the final gathering point. Moving the knight together with the king counts as a single move. 



Write a program to compute the minimum number of moves the player must perform to produce the gathering. 

Input

Your program is to read from standard input. The input contains the initial board configuration, encoded as a character string. The string contains a sequence of up to 64 distinct board positions, being the first one the position of the king and the remaining
ones those of the knights. Each position is a letter-digit pair. The letter indicates the horizontal board coordinate, the digit indicates the vertical board coordinate. 



0 <= number of knights <= 63

Output

Your program is to write to standard output. The output must contain a single line with an integer indicating the minimum number of moves the player must perform to produce the gathering.

Sample Input

D4A3A8H1H8

Sample Output

10

/**
poj 1178  floyd+枚举
题目大意：在一个8*8的棋盘里有一个国王和一些骑士，我们须要把他们送到同一顶点上去，骑士和国王的行动方式如图所看到的。国王能够选择一名骑士作为坐骑。上马后相当和该骑士
          一起行动（相当于一个骑士），同一位置能够同一时候有多个骑士和国王。问最少走的步数
解题思路：把8*8棋盘变成0~63的数，Floyd求出随意两点之间的最短路径。8*8枚举就可以。枚举终点，骑士上马点，国王上哪个骑士，终于负责度O(64^4)。
*/
#include <string.h>
#include <algorithm>
#include <iostream>
#include <stdio.h>
using namespace std;

char s[105];
int cx[8][2]= {{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}};
int dx[8][2]= {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
int a[65][65],b[65][65],rking[65],king;

bool judge(int i,int j)
{
    if(i>=0&&i<8&&j>=0&&j<8)
        return true;
    return false;
}

void init()
{
    for(int i=0; i<64; i++)
    {
        for(int j=0; j<64; j++)
        {
            if(i==j)
                a[i][j]=b[i][j]=0;
            else
                a[i][j]=b[i][j]=999;
        }
    }
    for(int i=0; i<8; i++)
    {
        for(int j=0; j<8; j++)
        {
            for(int k=0; k<8; k++)
            {
                int x=i+cx[k][0];
                int y=j+cx[k][1];
                int xx=i+dx[k][0];
                int yy=j+dx[k][1];
                if(judge(x,y))
                {
                    a[i+j*8][x+y*8]=1;
                }
                if(judge(xx,yy))
                {
                     b[i+j*8][xx+yy*8]=1;
                }
            }
        }
    }
    for(int k=0; k<64; k++)
    {
        for(int i=0; i<64; i++)
        {
            for(int j=0; j<64; j++)
            {
                a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
                b[i][j]=min(b[i][j],b[i][k]+b[k][j]);
            }
        }
    }
}
int main()
{
    init();
    while(~scanf("%s",s))
    {
        int n=strlen(s);
        king=s[0]-'A'+(s[1]-'1')*8;
        int cnt=0;
        for(int i=2; i<n; i+=2)
        {
            int x=s[i+1]-'1';
            int y=s[i]-'A';
            rking[cnt++]=x*8+y;
        }
        int ans=9999999;
        for(int i=0;i<64;i++)///终点
        {
            for(int j=0;j<64;j++)///国王上马点
            {
                for(int k=0;k<cnt;k++)///国王所上的骑士
                {
                    int sum=0;
                    for(int l=0;l<cnt;l++)
                    {
                        if(l==k)continue;
                        sum+=a[rking[l]][i];
                    }
                    sum+=b[king][j]+a[rking[k]][j]+a[j][i];
                    ans=min(ans,sum);
                }
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}