51nod 1197 字符串的数量 V2（矩阵快速幂+数论？）

　　接上一篇，那个递推式显然可以用矩阵快速幂优化...自己随便YY了下就出来了，学了一下怎么用LaTeX画公式，LaTeX真是个好东西！嘿嘿嘿

　　

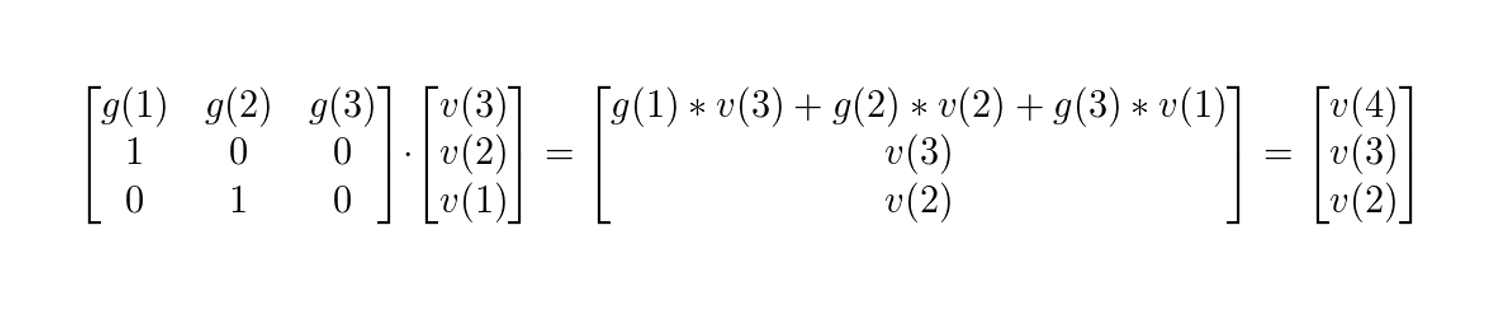
　　如上图。（刚画错了一发。。。已更新

　　然后就可以过V2了

　　orz CZL卡常大师，我怎么越卡越慢啊QAQ

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
const int maxn=,mod=1e9+;
int n,m,k;
int sum[maxn],v[maxn],g[],f[][maxn];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
int MOD(int x){return x>=mod?x-mod:x;}
int main()
{
    read(n);read(m);k=(int)floor(log(n)/log()+);
    for(int i=;i<=n;i++)f[][i]=,sum[i]=sum[i-]+;
    v[]=;g[]=n-((n>>)+)+;
    for(int i=;i<=k;i++)
    {
        for(int j=<<(i-);j<=n;j++)f[i][j]=sum[j>>];
        for(int j=(n>>)+;j<=n;j++)g[i]=MOD(g[i]+f[i][j]);
        sum[(<<(i-))-]=;for(int j=<<(i-);j<=n;j++)sum[j]=MOD(sum[j-]+f[i][j]);
    }
    for(int i=;i<=m;i++)
    {
        for(int j=;j<=min(i,k);j++)
        v[i]=MOD(v[i]+(1ll*g[j]*v[i-j]%mod));
    }
    printf("%d\n",v[m]);
    return ;
}