tricks

当 \(k>\sqrt{n}\) 的时候暴力跳，当 \(k<\sqrt{n}\) 的时候预处理。

调和级数哈希

主体思想：枚举长度 \(k\)，每次用哈希检测答案，复杂度 \(O(\sum \lfloor \dfrac{n}{k}\rfloor * H)\)，\(H\) 为哈希复杂度（一般是 \(O(1)\)，可能会有 \(log\)）

例题1 - 口胡题

例题2

例题1中，评论区神仙 @Tweetuzki 已经讲完了做法；

例题2中，枚举 \(k\) ，然后 \(O(n/k)\) 的跑一遍即可。然而这题还有一个问题，对于一个字符串，我们把它和它的反串视作本质相同的串，这咋哈希？

留到下一个trick里讲。

多属性哈希

主体思想：如果一个元素有若干种属性值，对于属性值一样的元素视作“本质相同的元素”，并且属性值很少；那我们可以把属性值的哈希值排一下序，然后序列哈希。

上一个trick留下的例题2

对于每个串，我们可以认为它有两个“属性值”：原串的哈希值，和反串的哈希值

我们把这两个值排一下序然后哈希即可...

两个数的哈希可以直接做：\((a,b) \rightarrow (a\times base+b)\bmod M\)

例题2代码

时光倒流

主体思想：一个序列, 或者一堆操作, 正着考虑不好整，就假装自己是小青蛙时光倒流，反过来考虑。

例1 经典题 [AHOI2005] 航线规划：树，删边，求点距离

逆向，删边变加边，随便做：树剖/LCT

例2 CF1366E Two Arrays：要求把序列 \(a\) 划分成 \(k\) 段，每一段的最小值递增，并且拼起来恰好是一个长度为 \(k\) 的另一个序列 \(b\)。给定 \(a,b\) ，求合法划分的方案数

最小值递增，那在段与段之间，每个段的最小值也是后缀最小值。那我们从后往前考虑，假设后缀最小值第一个等于 \(b_i\) 的位置是 \(p\)，并且后缀最小值等于 \(b_i\) 的一共有 \(k\) 个。显然它们会在同一个区间里。那么从这这一段区间里任选一个位置，划到 \(p\)，作为第 \(i\) 段，就可以满足条件。并且没有其他位置能满足条件。

所以答案就是，求出后缀最小值，求出数量数组cnt，\(\prod cnt_{b_i}\)

时光反复横跳

主体思想：“时光倒流”那个trick告诉我们可以反过来考虑，而如果有些必须正着完成的事情，先反过来一遍，用撤销的方法做回去。

例题：CF1416D

先反过来，得到最后删完的图；然后Kruskal重构树连回去，然后不断的撤销就可以了。每次找最大那个就用线段树瞎jb维护一下就行了。

主席树维护二分

主体思想：二分每次检测 \(mid\) 的时候序列都不一样，相邻的两个 \(mid\) 改变的并不多，用主席树全部存下来，再维护点啥，每次可以 \(O(log)\) 的检测。

这题暴力二分做法：

对于 \(mid\)，大于等于它的视为 \(1\)，其它的视为 \(-1\)，然后求 \([a,b]\) 区间的最大后缀和，\((b,c)\) 区间的和，\([c,d]\) 区间的最大前缀和，加起来即可。

我们发现这三个都能线段树维护。并且，对于 \(mid\rightarrow mid+1\)，只有原来 \(=mid\) 的地方从 \(1\) 变成了 \(-1\)。用 \(vector\) 记录下这些位置，每次修改，总修改次数是 \(n\) 次。直接主席树维护即可。

带上主席树复杂度就是 \(n\log n\)，即可求出 \(mid=[1,n]\) 时所有的检测用的数组。然后线段树区间和就可以 \(\log\) 的求，也就是 \(O(\log n)\) 检测一个 \(mid\)，套上二分复杂度就是 \(O(\log^2 n)\) 回答每个询问。

（这玩意还是个黑题，太水了吧

基环树上dp

主体思想：在环上随便钦定两个相邻的点，以两点为根跑树形 \(dp\)

这个做法有一些条件的...这题中，任意断一条边都对，才能这么做

如果断不同的边答案不一样，那就要枚举了，时间复杂度爆炸（有的题里可能不会

回到这题。这题里如果是一颗正常的树，显然是最大独立集问题。

然后我们随便钦定一个环上的 \(u,v\)，求 \(max(dp[u][0],dp[v][0])\)，即可

换根dp

主体思想：先求出以 \(u\) 为根的答案，然后再 \(dfs\) 一遍继承父亲的答案。

例题：树带权重心

先存储每个点往下的带权距离和。

去掉这个点对父亲的贡献，第二遍 \(dfs\) 的时候从父亲更新到儿子，以求出以每个点为根的带权距离和。

相对顺序不变

主体思想：变化是规律的，如果能证出来顺序不变，那直接二分即可

例：第 \(i\) 个数每次都加 \(a_i\)，初始为 \(0\)。显然这个顺序不变。每次要求某时刻多少个 \(>k\) 的，直接二分

线段树节点合并时二分

主体思想：左儿子和右儿子合并的时候，只有右儿子的一段前缀会没有，二分即可

例题：支持修改，求多少个数是前缀最大值

势能分析线段树

主体思想：线段树+优化暴力，用神奇的性质保证复杂度为 \(O(nlogn*K)\)

例题1：区间开根下取整，值域在 \([0,10^{12}]\)

每个数被开 \(6\) 次就变成 \(0/1\)，而 \(0/1\) 开根取整还是自己，于是不用管了；

于是这题复杂度是 \(O(K*nlogn)\)，其中 \(K_{max}=6\)

例题2：区间加正数，区间绝对值和

每个数只会在负变正的时候需要暴力讨论，其它时候绝对值都是-/+

于是 \(K_{max}=2\)，然后这题就是个sb题，代码略（其实是没写，百度抄一个

gcd 变 phi

主体思想：\((a,b)=\sum\limits_{d|a,d|b} \phi(d)\)

例：2020.10~11停课Day2 奇妙数论题

set 维护精确枚举

主体思想：用 set 存储合法的扩展，保证复杂度

例：2020.10~11停课Day2 CF920E

PS：例题中，把 \(set\) 部分的代码换成

F(i,1,n) if (!vis[i])

时间复杂度就变成了 \(O(n^2)\)

因数id

注：后设 \(D=\max \sigma_0(n)\)。它用来估算复杂度。

主体思想：当一个问题只涉及某个数 \(n\) 的因数时，我们可以把它的因数，从 \(1\) 开始重新编号，把规模转化为 \(\sigma_0(n)\)。注意，由于 \(D\) 很小，我们经常会需要处理一个大小为 \(D^2\) 的二维数组。

这在 \(n\le 10^9\) 时同样适用，因为此时 \(D=1344\)。

例1: arc004-4，问 \(n\) 能用多少种方法拆成 \(m\) 个整数的乘积。\(n\le 10^9,m\le 10^5\)

首先用组合方法求出安排符号的方案。然后注意到 \(>1\) 的数不会超过 \(\log n\) 个，然后剩下都是 \(1\)。用组合数方法求出安排 \(1\) 位置的方案。现在只需要求用 \(\le 30\) 个数拼出来 \(n\) 的方案数。

用上面那个 trick 求出每个因数的编号，设记下来第 \(i\) 个因数为 \(num[i]\)，因数 \(d\) 的编号为 \(id[d]\)。

设 \(dp[i][j]\) 表示选了 \(i\) 个因数拼出来 \(id=j\) 的方案数。枚举选多少个，枚举一个 \(id\) 为 \(x\)，枚举一个 \(id\) 为 \(y\)，用 dp[i-1][id[num[x]/num[y]]] 来更新 dp[i][x]。注意一个前提是 num[x] 是 num[y] 的倍数。

可我们并不能记下 \(id\)，每次求 \(id\) 还需要一次二分。这样直接转移带两个 \(\log\)（枚举选多少个是一个 \(\log\)，还有一个二分的 \(\log\)）。

考虑把二分的那一步预处理出来，设 rec_div[i][j] 表示 id(num[x]/num[y])。这样就省下一个 log，变为了可以通过的一个 \(\log\)。

例1代码

例2: noi.ac329 你要在一个 \(n\times m\) 的棋盘里，第一行选一个，中间行选一个或两个，最后一行选一个，使得乘积是 \(A\) 的倍数。输出方案数 \(\% H\) 。\(n\le 200,m\le 10^4,A\le 2\times 10^5, H\le 3\times 10^4\)

首先每个位置和 \(A\) 先取个 \(\gcd\)，这很显然。不是公因数的部分，去掉了也没有任何影响。

然后把 \(A\) 做一遍上面那个 trick，同样得到 \(id\) 与 \(num\)。不同的是这次 \(id\) 直接可以开下来数组。

接下来就 \(dp[i][j]\) 表示选到前 \(i\) 行乘积的 \(id=j\) 方案数。然而中间的行可以选两个数，而我们不能 \(O(m^2)\) 枚举，咋整？事实上我们可以先 \(O(m)\) 的枚举，记一个 \(cnt[i]\) 表示这一行中 \(id=i\) 的数个数。然后在 \(cnt\) 上 \(O(D^2)\) 转移。由于 \(D\) 很小，便省下了很多时间。

这里再注意一个细节，\(O(D^2)\) 转移的时候涉及到乘法，乘法完了还要再取一个 \(\gcd\) ，又会凭空多 \(\log\)。类似上面，设 \(mul[i][j]\) 表示 \(num[i]\times num[j]\) 和 \(A\) 取 \(\gcd\) ，省下每次做的 \(\log\)。

复杂度便是 \(O(nD^2+nm)\)

幂的意义

主体思想：把某个数的 \(k\) 次方，看成是选了 \(k\) 次一样的方案数。

例题：NOI2009管道取珠（经典，略）

不太常见

神秘

另类回文

主体思想：把平常写的 == 换成其它的匹配函数

在这题中，匹配函数为：

\[f(a,b)=
\begin{cases}
1 & (a \oplus b=1) \\
0 & \operatorname{else}
\end{cases}
\]

然后要你求有多少回文子串。

当然，这个 \(f\) 也可以是任意神奇的函数

↑ 这句话是假的，\(f\) 必须要满足一些性质：

对于任意两个长度相同的串 \(a,b\)，对于所有 \(1\le i\le |a|\)，满足 \(f(a_i,b_i)=1\)，则有：\(a,b\) 两串回文等价。

两个串回文等价定义为，“是否回文”这个bool值相同。

这个题中，如果 \(f(a_i,b_i)=1\)，那么 \(a\) 和 \(b\) 恰好是二进制取反的关系，注意到 \(f\) 比较函数中两字符同时取反不会影响 \(f\) 的值，所以 \(a,b\) 显然是回文等价的。

然后我们把这个函数处理出来跑 Manacher 就可以了。它可以求出以任意点为中心的最长回文半径。这样就可以求出最长的回文子串长度，以及回文子串的种类数。

维护差量

主体思想：把一个数的贡献，看成是初始一个数，不断的叠上去。枚举叠上去的“层”，叠加贡献。它的本质是，从按列求和变成按行求和。

可以用这个图来描述：

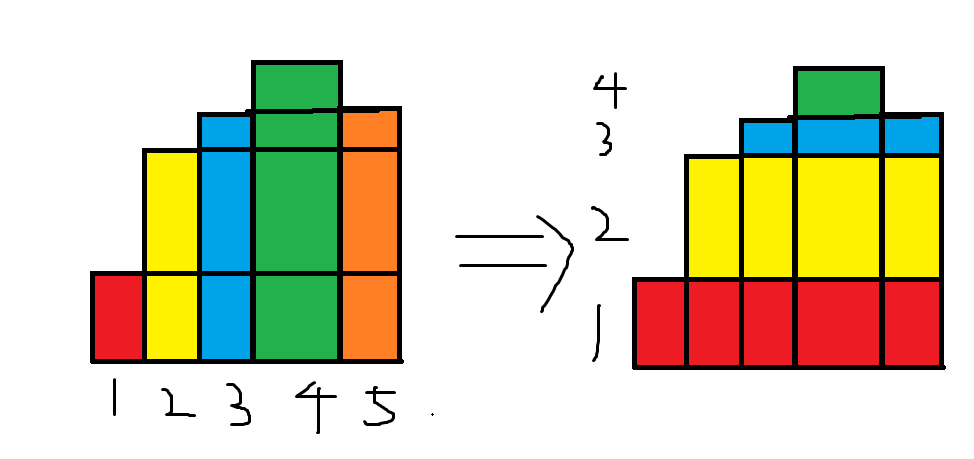
例题1: 集合

设 \(k\) 的答案为 \(f_k\)

一方面，直接钦点最小值，答案是

\[f_k=\sum\limits_{i=1}^{n} T^i \times \binom{n-i}{k-1}
\]

另一方面，分段枚举最小值，并累计差量（即这个trick），答案也是

\[T\times \binom{n}{k} + \sum\limits_{i=1}^{n-1} (T^{i+1}-T^i)\times \binom{n-i}{k}
\]

（先特判 \(\ge 1\) 的情况，后面枚举的 \(i\) 表示最小值 \(>i\)）

后面的式子提一个 \(T^i\) 出来，发现它就是 \(f_{k+1}\)（注意到这里的 \(\sum\) 可以取到 \(n\)，这时候后面的组合数为 \(0\)，不影响）

于是有 \(f_k=T\binom{n}{k}+(T-1)f_{k+1}\)

显然有 \(f_n=T\) 。不断用这个式子，从 \(k\) 变到 \(n\)，手推几个即可发现：

\[f_k=\sum\limits_{i=0}^{n-k} T(T-1)^i\times \binom{n}{k+i}
\]

再来点变换：\((T-1)^i=\dfrac{(T-1)^{k+i}}{(T-1)^k}\) （显然），然后把常数 \((T-1)^k\) 和 \(T\) 提到 \(\sum\) 的外面

变成：

\[f_k=\dfrac{T}{(T-1)^k} \sum\limits_{i=0}^{n-k} (T-1)^{i+k}\times \binom{n}{i+k}\\
=\dfrac{T}{(T-1)^k} \sum\limits_{i=k}^{n} (T-1)^{i}\times \binom{n}{i}\\
\]

我们注意到后面的式子，和二项式定理的式子，只差了 \(k\) 项。而 \(k\) 很小，只有 \(1e7\)，于是预处理阶乘，逆元，阶乘逆元等，暴力算出这 \(k\) 项，用二项式定理化成的 \(A^n\) 减去这 \(k\) 项的和，就可以得到后面的，再加上前面的即可求出和，然后除一个 \(\binom{n}{k}\) 得期望。

数论域的 log

主体思想：\(\log(ab)=\log(a)+\log(b)\)，质因子个数函数 \(\omega\) 和它有相同的性质。

例：2020.10~11停课Day2 狄利克雷卷积k次根

幂分类讨论

主体思想：答案与指数函数有关，并且要最小化。这时，当幂小的时候暴力做，幂大的时候，优先让指数小，再让别的小，转化成双关键字的最小化问题。

和根号分治的思想有几分类似，大数据和小数据两种方法做。

例：CF1442C Graph Transpositions：一张有向图上要从 \(1\) 走到 \(n\)，走边花费都是 \(1\)。每次走一条边都可以选择是否对 所有的边 做一次反向操作。如果一共做 \(t\) 个反向操作，花费为 \(2^t-1\)。输出最小的从 \(1\) 走到 \(n\) 的总花费，模 \(998244353\)。先最小，再取模。\(n\le 2e5\)

假设 \(t\ge 20\)，那么每增加一个 \(t\) 的花费就是 \(1e6\) 级别的，这比在图上随便走都来的大。对于这种情况，把有向边 \((u,v)\) 看成是：\(u\rightarrow v,w=(0,1)\) ；\(v\rightarrow u,w=(1,1)\)。然后跑一个双关键字最短路，假设最短边权和为 \((a,b)\) ，实际答案为 \((2^a-1)+b\)。

细节：这里要分一下奇偶讨论，因为翻转了奇数次和偶数次的时候，边的正反就会不一样，然后边权的第一关键字就要相应的有变化。

双关键字最短路就是每条边的权是一个二元组，然后要先让第一关键字的和最小，在此基础上再让第二关键字的和最小

做法非常simple，就是dijkstra的时候记在priority_queue里的东西从int变成pair<int,int>就行了。如果想方便可以再重载一个+运算符，然后就和普通最短路几乎一模一样了

假设 \(t\le 20\)，设 \(d(i,k)\) 表示走到 \(i\) ，翻转了 \(k\) 次的最短路。这个可以暴力做，复杂度是 \(O(20n \times \log 20n)\) （本质是一个分层图）。

总的复杂度就是 \(O(20n\log n)\) 了。\(2e5\)，随便过。