曲线生成与求交—Bezier曲线

Bezier曲线生成

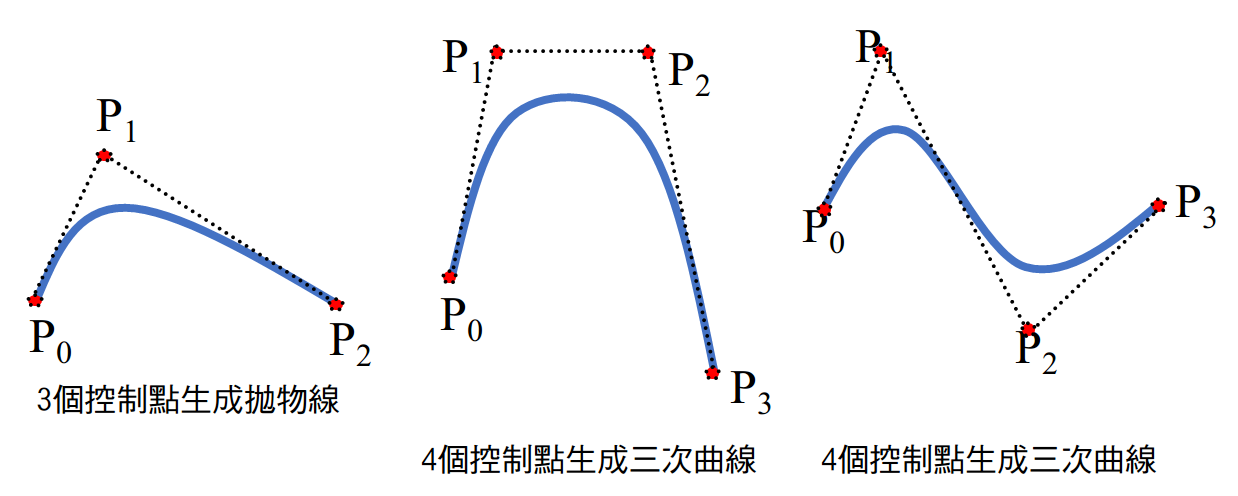
法国工程师Pierre Bezier在雷诺公司使用该方法来设计汽车。一条Bezier曲线可以拟合任何数目的控制点。

公式

设\(n+1\)个控制点\(P_0,P_1……P_n\)，其中$P_k=(X_k,Y_k,Z_k),0≤k≤n $

则\(n\)次Bezier曲线为：

\[P(t)=∑P_iB_{i,n}(t)\qquad 0≤t≤1
\]

其中，\(B_{i,n}(t)\)是Bernstein基函数，即

\[B_{i,n}(t)=c_n^it^i(1-t)^{n-i}\\
c_n^i=\frac {n!}{i!(n-i)!}\quad i=0,1,2\cdots n
\]

Bezier曲线的特性

在贝塞尔曲线中，只有起点和终点在曲线上

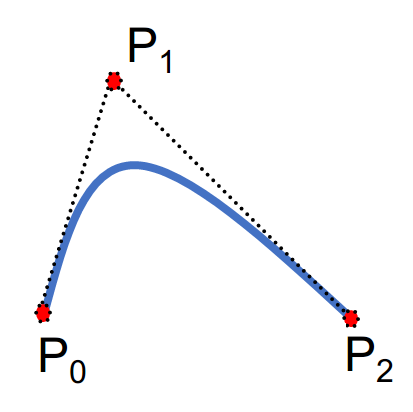
曲线在两个端点处的边界条件：

\[P(0)=P_0,P(1)=P_n
\]

证明：

\[\begin{align*}\label{}
&P(0)= ∑PiB_{i,n}(t)= ∑PiB_{i,n}(0)\\
&B_{i,n}(0)= c_n^it^i(1-t)^{n-i}=c_n^i0^i\\
&i=0时0^0=1\\
&B_{0,n}(0)=cn0=1\\
&B_{i,n}(0)=0\quad (i≠0时)\\
&∴ P(0)=P_0 \\
\end{align*}
\]

\[\begin{align*}\label{}
&P(1)= ∑P_iB_{i,n}(1)\\
&B_{i,n}(1)= c_n^i1^i(1-1)^{n-i}\\
&B_{n,n}(1)=c_n^n1^n0^0=1\quad (i=n时)\\
&B_{i,n}(1)=0\quad (i≠n时)\\
&∴P(1)=Pn
\end{align*}
\]

曲线起点的切线在头两个控制点连线上，曲线终点的切线在最后两个控制点连线上。

Bezier曲线在端点处的一阶导数值可以由控制点坐标计算：

\[ P’(0)=-nP_0+nP_1=n(P_1-P_0)\\
P’(1)=-nP_{n-1}+nP_n
\]

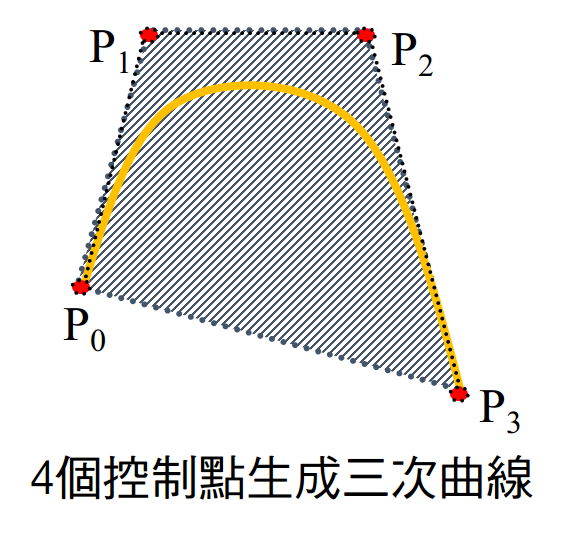
Bezier曲线落在控制点的凸包内（凸多边形边界）

三次Bezier曲线

三次Bezier曲线由四个控制点生成。

当n=3时，

\[\begin{align*}\label{}
&B_{i,3}(t)=c_3^it^i(1-t)^{3-i}\quad i=0,1,2,3\\
&B_{0,3}(t)=c_3^0t^0(1-t)^{3-0}=(1-t)3\\
&B_{1,3}(t)=3t(1-t)^2\\
&B_{2,3}(t)=3t^2(1-t)\\
&B_{3,3}(t)=t^3\\
\end{align*}
\]

则：

\[\begin{aligned}
P(t)= ∑P_iB_{i,3}(t)
&=P_0B_{0,3}(t)+ P_1B_{1,3}(t)+ P_2B_{2,3}(t)+ P_3B_{3,3}(t) \\
&=
\begin{bmatrix}
B_{0,3}(t) & B_{1,3}(t) & B_{2,3}(t) & B_{3,3}(t)
\end{bmatrix}
\begin{bmatrix}
P_0 \\ P_1 \\ P_2 \\ P_3
\end{bmatrix}
\\
&= \begin{bmatrix}
t^3 & t^2 &t & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1\\
3& -6 & 3 & 0\\
-3 & 3 & 0 & 0\\
1& 0& 0& 0
\end{bmatrix}
\begin{bmatrix}
P_0 \\ P_1 \\ P_2 \\ P_3
\end{bmatrix}
\end{aligned}
\]

那么，\(x(t)\)和\(y(t)\)分别为：

\[\begin{aligned}x(t) &= \begin{bmatrix} t^3 & t^2 &t & 1\end{bmatrix}\begin{bmatrix}-1 & 3 & -3 & 1\\ 3& -6 & 3 & 0\\ -3 & 3 & 0 & 0\\ 1& 0& 0& 0\end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\x_2 \\ x_3\end{bmatrix}\end{aligned}
\]

\[\begin{aligned}
y(t)
&= \begin{bmatrix}
t^3 & t^2 &t & 1
\end{bmatrix}
\begin{bmatrix}
-1 & 3 & -3 & 1\\
3& -6 & 3 & 0\\
-3 & 3 & 0 & 0\\
1& 0& 0& 0
\end{bmatrix}
\begin{bmatrix}
y_0 \\y_1 \\y_2 \\ y_3
\end{bmatrix}
\end{aligned}
\]

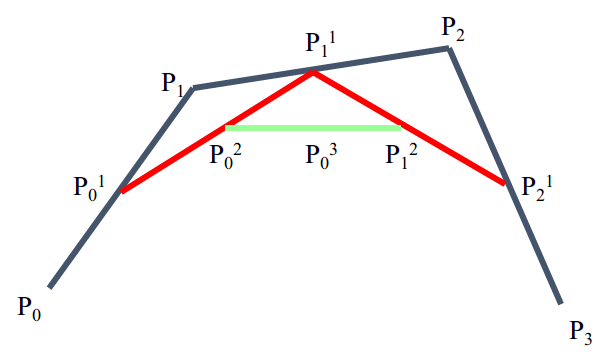
Bezier曲线的Casteljau算法

给定三维空间点\(P_0,P_1,\cdots ,P_n\)以及一维标量参数\(t\)，假定：

\[P_i^r(t)=(1-t)P_i^{r-1}(t)+tP_{i+1}^{r-1}(t)\qquad
\left\{\begin{matrix}
r=1,\cdots ,n\\
i=0,\cdots ,n-4
\end{matrix}\right.
\]

并且\(P_i^0(t)=P_i\)

那么\(P_i^n(t)\)即为Bezier曲线上参数\(t\)处的点

三次Bezier曲线的分割递推算法

\[P_0^1(t) = (1-t)P_0^0(t)+tP_1^0(t)
\]

\[P_1^1(t) = (1-t)P_1^0(t)+tP_2^0(t)
\]

\[P_2^1(t) = (1-t)P_2^0(t)+tP_3^0(t)
\]