RSA脚本环境配置-攻防世界-OldDriver

【Crypto】题目链接【RSA算法解密】

审题分析

首先拿到一个压缩包，解压得到文件enc.txt。先不用去管其他，第一眼enc马上联想到 RSA解密。接着往下看

[{"c": 7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n": 25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},

{"c": 21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n": 23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},

{"c": 6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n": 18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},

{"c": 4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n": 23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},

{"c": 22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n": 31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},

{"c": 17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n": 22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},

{"c": 1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n": 25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},

{"c": 15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n": 32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},

{"c": 8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n": 52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},

{"c": 13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n": 30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]

给出十组RSA（enc）加密信息。且十组的e都相同。这里涉及到三个参数：

e / c ：c要满足： e * c = 1 (mod(p-1) * (q-1))

n : n = p * q（p和q是两个不同的大素数）

{ e , n } 为公开密钥 { c , n } 为私有密钥

详情可参考阮一峰RSA算法

低加密指数广播攻击

推一波大佬的总结：详情戳这里

低加密指数广播攻击

介绍：

如果选取的加密指数较低，并且使用了相同的加密指数给一个接受者的群发送相同的信息，那么可以进行广播攻击得到明文。

即，选取了相同的加密指数e（这里取e=3），对相同的明文m进行了加密并进行了消息的传递，那么有：

$ c_1equiv m^e$ $mod$ $n_1$

$ c_2equiv m^e$ $mod$ $n_2$

$ c_3equiv m^e$ $mod$ $n_3$

对上述等式运用中国剩余定理，在e=3时，可以得到：

$ c_xequiv m^3$ $mod$ $n_1n_2n_3$

通过对$ c_x $进行三次开方可以求得明文。

识别：

这个识别起来比较简单，一般来说都是给了三组加密的参数和明密文，其中题目很明确地能告诉你这三组的明文都是一样的，并且e都取了一个较小的数字。

环境准备

python2.x -- python3.x 环境准备
libnum
gmpy2（重头戏）

`python2.x -- python3.x` 环境准备

第一个相信大家都已经准备好了。

安装 libunm

如何下载 libunm库 只需打开 cmd 窗口，执行该命令即可：

pip install libnum -i https://pypi.mirrors.ustc.edu.cn/simple/

-i 后面接的是镜像源，加速下载。可以换源自取。

阿里云 http://mirrors.aliyun.com/pypi/simple/

中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/

豆瓣(douban) http://pypi.douban.com/simple/

清华大学 https://pypi.tuna.tsinghua.edu.cn/simple/

中国科学技术大学 http://pypi.mirrors.ustc.edu.cn/simple/

若是下载失败或者在pycharm里运行还是显示没有该模块，则我们可以采取直接法。直接在pycharm里下载该库。

先打开pycharm -> settings -> Project Interpreter -> "+" -> 输入 libnum ->下载 -> 完成。

这里提一句：点击下方红框按钮，进行添加镜像，下载速度会更快哦~镜像源在上面已经给出，可自取！

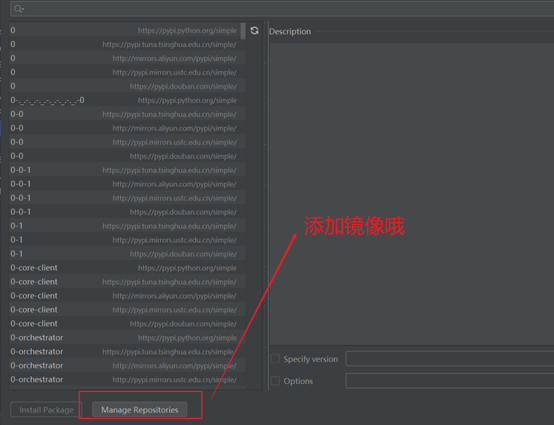
若出现不信任报错，手动修改 http 为 https 即可！

顺带一提：在做RSA解题时经常会碰到 import crypto 如题【攻防世界】 cr3-what-is-this-encryption

import libnum

from Crypto.Util.number import long_to_bytes

安装pycryptodome

缺少crypto模块怎么办？

法一： pip 安装

法二： pycharm 里直接安装 crypto ，发现找不到？！实际上应安装 pycrypto 即可。

(法一法二均与上述libnum模块安装一致)

法三：pycharm里面直接安装 pycryptodome 模块

（PS：像博主这种倒霉蛋pycrypto又没安成功，只好曲线救国）

这样就万事大吉啦~~

Windows下 -- gmpy2安装

最后一项下载 gmpy2库 这可真是太折腾了。博主亲测：

第一种：与上述装 libnum库一样，直接 pip 或者 pycharm 里安装。（反正倒霉蛋我是不行的）
第二种：利用pip 安装 .whl 轮子文件成功上岸！！

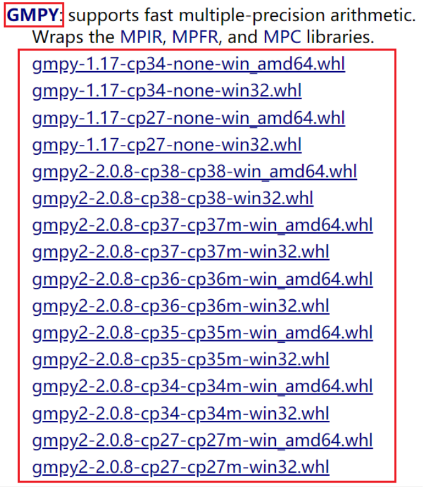
首先，确定自己的python 版本，可直接用 python -version 查看。

下面，来这个宝藏之地找到 GMPY 板块。根据自己的python版本来进行相应的下载。

比如说，博主的python环境是 python3.8 ，并且，电脑是64版本，那就下载相对应的 gmpy2‑2.0.8‑cp38‑cp38‑win_amd64.whl 的文件即可。

安装后，进入你安装的python环境的目录。打开 Script 文件夹，将刚下载好的.whl文件拖进去，然后在此处打开 cmd窗口，或者是 Powershell 。执行以下命令：注意！！.whl文件名一定要复制完整！！

C:\Program Files\Python38\Scripts> pip install gmpy2‑2.0.8‑cp38‑cp38‑win_amd64.whl

这样就安装成功啦！！

Kali Linux下安装 RsaCtfTools

RsaCtfTools 也是解Rsa题目的必备神器。如何安装，大家可以康康大佬的这篇 kail下安装RsaCtfTool

(博主亲测安装很顺利)

但是！！在安装mpfr时，记得将命令换成这条哦！不然会404
wget https://www.mpfr.org/mpfr-current/mpfr-4.1.0.tar.bz2
在执行 pip install -r requirements.txt 时，记得先返回 RsaCtfTool目录中哦
cd ../

cd ../
友情提醒一下 RsaCtfTool.py 是 python3 哒

python2 pip 安装：
apt-get install python-pip
python3 pip3 安装：
apt-get install python3-pip
python -V 查看当前版本~

Successful!!!

解题脚本

万事俱备，只欠东风~接下来可以解题了。利用中国剩余定理来进行编写解密脚本借鉴网上大佬脚本：这里

python3.x 脚本

import libnum

import gmpy2

dic =[{"c":7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n":25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},

{"c":21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n":23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},

{"c":6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n":18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},

{"c":4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n":23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},

{"c":22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n":31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},

{"c":17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n":22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},

{"c":1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n":25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},

{"c":15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n":32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},

{"c":8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n":52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},

{"c":13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n":30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]

n = []

C = []

for i in dic:

    n.append(i["n"])

    C.append(i["c"])

N = 1

for i in n:

    N *= i

Ni = []

for i in n:

    Ni.append(N // i)

T = []

for i in range(10):

    T.append(int(gmpy2.invert(Ni[i], n[i])))

X = 0

for i in range(10):

    X += C[i] * Ni[i] * T[i]

m10 = X % N

m = gmpy2.iroot(m10, 10)

print (libnum.n2s(m[0]))

python2.x 脚本

import libnum

import gmpy2

dic =[{"c":7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n":25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},

{"c":21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n":23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},

{"c":6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n":18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},

{"c":4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n":23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},

{"c":22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n":31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},

{"c":17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n":22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},

{"c":1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n":25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},

{"c":15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n":32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},

{"c":8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n":52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},

{"c":13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n":30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]

n = []

C = []

for i in dic:

    n.append(i["n"])

    C.append(i["c"])

N = 1

for i in n:

    N *= i

Ni = []

for i in n:

    Ni.append(N / i)

T = []

for i in xrange(10):

    T.append(long(gmpy2.invert(Ni[i], n[i])))

X = 0

for i in xrange(10):

    X += C[i] * Ni[i] * T[i]

m10 = X % N

m = gmpy2.iroot(m10, 10)

print libnum.n2s(m[0])

python2.x和python3.x环境脚本存在三个不同

print 有无括号（不提也罢）

Ni.append(N / i) 在Python3中，N / i 返回的是float类型，float 最大值为1.7976931348623157e+308 因此会报错 OverflowError: integer division result too large for a float 所以要将它绕过，用//代替/，这样返回的是Integer 。

T.append(long(gmpy2.invert(Ni[i], n[i]))) 在Python3中，不存在 long() 函数，直接改为 int() 就可

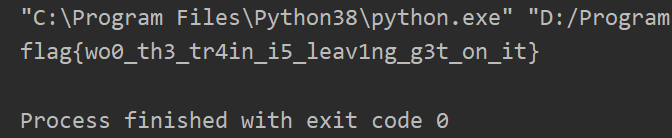
综上！！得到flag啦~~

flag{wo0_th3_tr4in_i5_leav1ng_g3t_on_it}

结语

关于以上链接引用【侵权删】

第一次写博客，多多担待！若有错误之处还请多多指正~!

【转载请放链接】 https://www.cnblogs.com/Jlay/p/RSA_Environment.html