Jack Straws(POJ 1127)

• 原题如下：
  Jack Straws

  Time Limit: 1000MS		Memory Limit: 10000K
  Total Submissions: 5555		Accepted: 2536

  Description

  In the game of Jack Straws, a number of plastic or wooden "straws" are dumped on the table and players try to remove them one-by-one without disturbing the other straws. Here, we are only concerned with if various pairs of straws are connected by a path of touching straws. You will be given a list of the endpoints for some straws (as if they were dumped on a large piece of graph paper) and then will be asked if various pairs of straws are connected. Note that touching is connecting, but also two straws can be connected indirectly via other connected straws.

  Input

  Input consist multiple case,each case consists of multiple lines. The first line will be an integer n (1 < n < 13) giving the number of straws on the table. Each of the next n lines contain 4 positive integers,x1,y1,x2 and y2, giving the coordinates, (x1,y1),(x2,y2) of the endpoints of a single straw. All coordinates will be less than 100. (Note that the straws will be of varying lengths.) The first straw entered will be known as straw #1, the second as straw #2, and so on. The remaining lines of the current case(except for the final line) will each contain two positive integers, a and b, both between 1 and n, inclusive. You are to determine if straw a can be connected to straw b. When a = 0 = b, the current case is terminated.

  When n=0,the input is terminated.

  There will be no illegal input and there are no zero-length straws.

  Output

  You should generate a line of output for each line containing a pair a and b, except the final line where a = 0 = b. The line should say simply "CONNECTED", if straw a is connected to straw b, or "NOT CONNECTED", if straw a is not connected to straw b. For our purposes, a straw is considered connected to itself.

  Sample Input

  7
  1 6 3 3
  4 6 4 9
  4 5 6 7
  1 4 3 5
  3 5 5 5
  5 2 6 3
  5 4 7 2
  1 4
  1 6
  3 3
  6 7
  2 3
  1 3
  0 0
  
  2
  0 2 0 0
  0 0 0 1
  1 1
  2 2
  1 2
  0 0
  
  0

  Sample Output

  CONNECTED
  NOT CONNECTED
  CONNECTED
  CONNECTED
  NOT CONNECTED
  CONNECTED
  CONNECTED
  CONNECTED
  CONNECTED

• 题解：问题的关键是判断线段是否相交，然后就可以建图进行连接性判断。首先会想到计算两直线的交点然后判断交点是否在线段上的方法，这样问题就变成如何判断点是否在线段上以及如何求两直线的交点。在几何问题中，运用向量的内积和外积进行计算是非常方便的。对于二维向量p₁=(x₁,y₁)和p₂=(x₂,y₂)，定义内积p₁·p₂=x₁x₂+y₁y₂，外积p₁×p₂=x₁y₂-y₁x₂。要判断点q是否在线段p₁-p₂上，只要先根据外积(p₁-q)×(p₂-q)是否等于0来判断点q是否在直线p₁-p₂上，再利用内积(p₁-q)·(p₂-q)是否小于等于0来判断点q是否落在p₁-p₂之间。而要求两直线的交点，通过变量t将直线p₁-p₂上的点表示为p₁+t(p₂-p₁)，交点又在直线q₁-q₂上，所以有：(q₂-q₁)×(p₁+t(p₂-p₁)-q₁)=0，于是可以利用下式求得t的值：
  
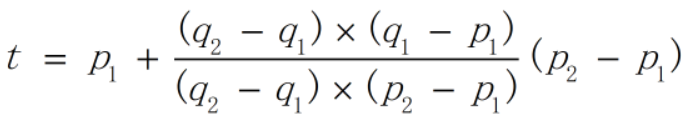
  但是，使用这个方法还要注意边界情况，如果两条线段是平行的，也有可能有公共点，可以通过检查端点是否在另一条线段上来判断。
• 代码：

   #include <cstdio>
   #include <cmath>
   #include <algorithm>
  
   using namespace std;
  
   const double EPS=1e-;
  
   double add(double a, double b)
   {
       if (fabs(a+b)<EPS*(fabs(a)+fabs(b))) return ;
       return a+b;
   }
  
   struct P
   {
       double x,y;
       P(){};
       P(double x, double y):x(x),y(y){}
       P operator + (P p)
       {
           return P(add(x, p.x), add(y, p.y));
       }
       P operator - (P p)
       {
           return P(add(x, -p.x), add(y, -p.y));
       }
       P operator * (double d)
       {
           return P(x*d, y*d);
       }
       double dot(P p)
       {
           return add(x*p.x, y*p.y);
       }
       double det(P p)
       {
           return add(x*p.y, -y*p.x);
       }
   };
  
   bool on_seg(P p1, P p2, P q)
   {
       return (p1-q).det(p2-q)== && (p1-q).dot(p2-q)<=;
   }
  
   P intersection(P p1, P p2, P q1, P q2)
   {
       return p1+(p2-p1)*((q2-q1).det(q1-p1)/(q2-q1).det(p2-p1));
   }
  
   const int MAX_N=;
   const int MAX_M=;
   int n;
   P p[MAX_N], q[MAX_N];
   int m;
   int a[MAX_M], b[MAX_M];
   bool g[MAX_N][MAX_N]; 
  
   int main()
   {
       while (~scanf("%d", &n) && n)
       {
           fill(g[], g[]+sizeof(bool)**, false);
           for (int i=; i<n; i++)
           {
               scanf("%lf %lf %lf %lf", &p[i].x, &p[i].y, &q[i].x, &q[i].y);
           }
           for (int i=;;i++)
           {
               scanf("%d %d",&a[i], &b[i]);
               if (a[i]== && b[i]==)
               {
                   m=i;
                   break;
               }
           }
           for (int i=; i<n; i++)
           {
               g[i][i]=true;
               for (int j=; j<i; j++)
               {
                   if ((p[i]-q[i]).det(p[j]-q[j])==)
                   {
                       g[i][j]=g[j][i]=on_seg(p[i], q[i], p[j])
                                    || on_seg(p[i], q[i], q[j])
                                    || on_seg(p[j], q[j], p[i])
                                    || on_seg(p[j], q[j], q[i]);
                   }
                   else
                   {
                       P r=intersection(p[i], q[i], p[j], q[j]);
                       g[i][j]=g[j][i]=on_seg(p[i], q[i], r) && on_seg(p[j], q[j], r);
                   }
               }
           }
           for (int k=; k<n; k++)
               for (int i=; i<n; i++)
                   for (int j=; j<n; j++)
                   {
                       g[i][j] |= g[i][k]&&g[k][j];
                   }
           for (int i=; i<m; i++)
           {
               puts(g[a[i]-][b[i]-] ? "CONNECTED" : "NOT CONNECTED");
           }
       }
   }