Top Coder 某场Div 2的C题 题解

前天，我们了解了一下一种叫做树状数组的神奇玩意儿，今天就放一道真题来检验一下自己的学习成果吧！

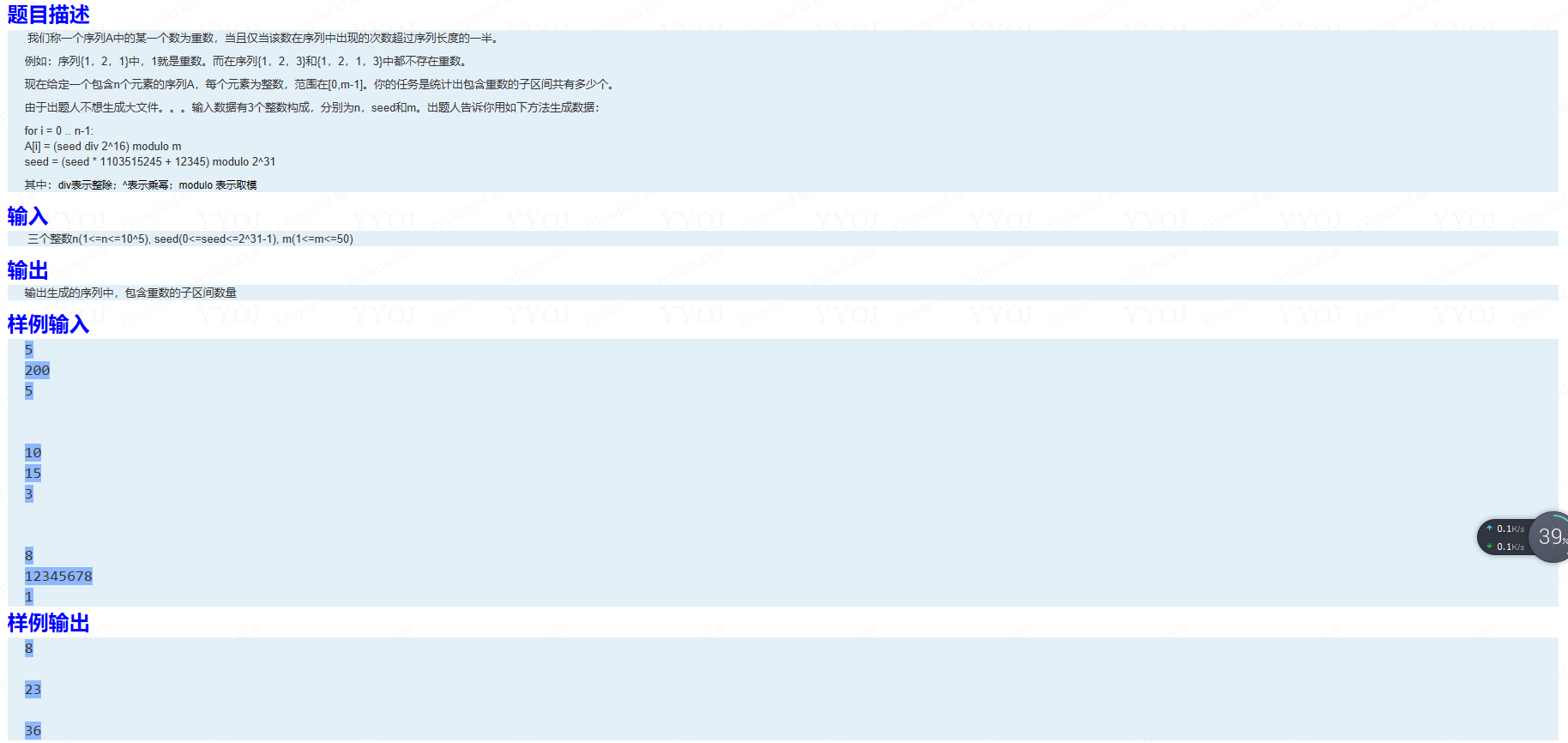
嗯，题目就是这样的啦。

分析：

这题的暴力大家应该都会打吧。

注意到m小的压批，所以对于每一个m值，我们可以用前缀和求出[1,i]这个区间内值为m的数的数量，然后在枚举每个区间，判断一下就OK了。这就是暴力，注意到时间复杂度为(n²m)的。

根据复杂度，我们可以知道，只要再优化掉一个n，或者把n优化成log，那么问题就解决了。

那么这个优化应该如何来进行呢？

我们可以先把数列进行重构：对于a[i]的每一个取值k，进行一次重构，a[i]=k，就把a[i]赋值为1，否则就为-1，那么对于一个区间[l,r]，只要sum[r]-sum[l-1]>0那么这个区间就是合法的。（sum为前缀和数组）

重构数列完成后，我们思考：在暴力算法中，枚举区间，枚举了两个端点，那么我们能否做到只枚举一个端点，然后用log的时间求出所有合法右端点的数量，累计到答案上。

至于枚举的那个端点，毫无疑问，是右端点（好吧，只是为了方便，闲着蛋疼的同学也可以尝试着去枚举左端点），然后我们注意到，所有sum值小于sum[r]的，都可以是一个合法的左端点，你是否想到了什么呢？——我*，树状数组直接上啊！！！（也可以是权值线段树）

在枚举r（右端点）的同时，将每个sum[r]加入树状数组，其中，sum[r]为元素下标，加的值为1，然后给ans（答案）加上Getsum(sum[r]-1)就行了。（Getsum（x）为用树状数组求出所有sum值在[1,x]中的数量）

代码：

var
  a:array[1..100000]of int64;
  sum:array[0..100000]of longint;
  c:array[0..200010]of longint;
  i,j,k:longint;
  n,seed,m,ans:int64;
procedure update(x,y:longint);
begin
  if x<200010 then begin c[x]:=c[x]+y; update(x+x and(-x),1) end else exit;
end;
function getsum(x:longint):longint;
begin
  if x>0 then exit(c[x]+getsum(x-x and(-x))) else exit(0);
end;
begin
  read(n,seed,m);
  for i:=1 to n do
  begin
    a[i]:=(seed div 65536)mod m;
    seed:=(seed*1103515245+12345)mod 2147483648;
  end;
  for i:=0 to m-1 do
  begin
    fillchar(c,sizeof(c),0);
    sum[0]:=100005; update(sum[0],1);                                           //这里特别注意把sum[0]赋值为100000+，因为树状数组在下标<=0时会炸！
    for j:=1 to n do
    begin
      if a[j]=i then sum[j]:=sum[j-1]+1 else sum[j]:=sum[j-1]-1;
      update(sum[j],1);
      ans:=ans+getsum(sum[j]-1);
    end;
  end;
  writeln(ans);
end.