【有向图】强连通分量-Tarjan算法

好久没写博客了（都怪作业太多，绝对不是我玩的太嗨了）

所以今天要写的是一个高大上的东西：强连通

首先，是一些强连通相关的定义　　//来自度娘

1.强连通图（Strongly Connected Graph）是指在有向图G中，如果对于每一对vi、vj，vi≠vj，从vi到vj和从vj到vi都存在路径，则称G是强连通图。

2.有向图的极大强连通子图，称为强连通分量(strongly connected components)。

当然，看定义是肯定看不懂的，所以，我举个栗子说明一下

我们以下图为例，这是一个特别经典的强连通图，三个被框起来的地方就分别是三个强连通分量

我们DFS一下，从一出发，我们从右至左遍历，所以路径便是1——>3——>5——>6，到了6，我们发现无路可走了，就回到5，而6不能到达任何一个点，所以它独自为一个强连通分量。同理，5也是一个强连通分量。而1——>3——>4——>1——>2，可以互相到达，所以这又是一个强连通分量。

Tarjan算法

接下来，就是一个在强连通中，常用的一个算法。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

接下来演示一下算法：

从1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

返回到5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

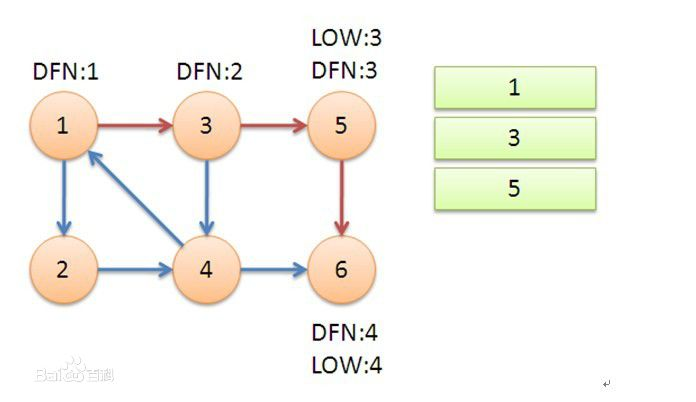
继续回到1，最后访问2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

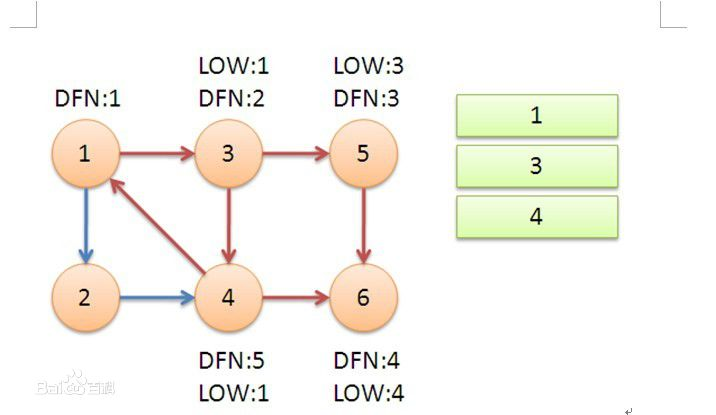
所以，三个强连通分量全部都找出来了。

模板如下：

 void Tarjan(int u){
     dfn[u]=low[u]=++num;
     st[++top]=u;
     for (int i=fir[u]; i; i=nex[i]){
         int v=to[i];
         if (!dfn[v]){
             Tarjan(v);
             low[u]=min(low[u],low[v]);
         }
         else if (!co[v])
             low[u]=min(low[u],dfn[v]);
     }
     if (low[u] == dfn[u]){
         co[u]=++col;
         while (st[top]!=u){
             co[st[top]]=col;
             --top;
         }
         --top;
     }
 }