Labview学习之路(十一)日常编程技巧

此文章用于记录自己在学习Labview过程中所用到的编程技巧，会一直更新下去。

（一）移动控件

1. 直接鼠标拖动。
2. 按住shift键，鼠标移动，可以水平和竖直移动（取决于鼠标最开始的移动方向）。
3. 使用键盘的方向键，移动步长小，可以做到精确移动对象。
4. 键盘方向键加shift键可以实现快速移动。

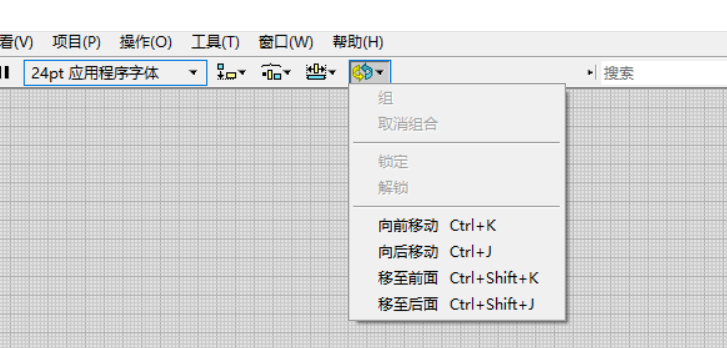
（二）组合和锁定

1. 当多个控件功能类似时，一个一个的移动会造成很多麻烦，我们可以让他们组成一个统一的整体，称为“组合”，这样他们移动就会一起移动，很方便。
2. 当你不想移动控件，可以把他们进行锁定，这样鼠标就不能再移动控件了，想移动的话进行解锁就可以了
3. 上述两个功能都在前面板 帮助 的下边的重新排序中

好处：当一个模块编写好后，组合和锁定可以有效的规避错误。

（三）固定控件选版

1. 如果觉得控件太多，每次都要右键点击。那就点控件选版左上角的图钉按钮，他就会固定住，方便选择。函数面板同样。

（四）前面板控件发灰

1. 表明该元素不可用，而不是0.

（五）变量

数据流的运行速度高于局部变量，数据流和局部变量运行速度高于属性节点。

局部变量和群居变量最大问题是数据竞争，尽量避免使用。