BZOJ5093 图的价值（NTT+斯特林数）

显然每个点会提供相同的贡献。于是现在只考虑1号点的贡献。若其度数为i，则在2~n号点选i个连上，剩下的边随便连，这样可以算出答案为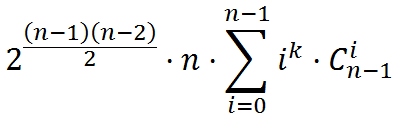

这个式子可以O(n)计算。发现k比较小，于是考虑如何将这个式子化为与k有关的求和。

显然前面一部分可以直接提走。考虑后面一部分的组合意义：n-1个有标号盒子里面选i个，放进去k个球的方案数

可以对这个过程进行变换：把k个球放在n-1个有标号盒子里，有球的盒子必须选，没有的可选可不选的方案数

枚举有球的盒子有多少个，可以发现答案变成了一个与k有关的式子：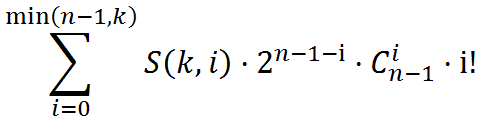

S(k,i)为第二类斯特林数，也即将k个小球放进i个盒子（每个盒子非空）的方案数。

问题变为快速求斯特林数。可以用容斥原理推导出斯特林数卷积形式的通项公式：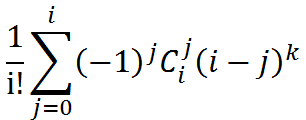

即给盒子标上号，枚举有几个空盒。再化一下：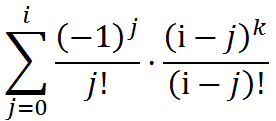

这样卷积形式就很明显了。用NTT算一下即可。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
#define P 998244353
#define N 300000
int n,k,a[N],v[N<<],s[N<<],inv[N],ans,ans2;
int t,r[N<<];
int ksm(int a,int k)
{
    if (k==) return ;
    int tmp=ksm(a,k>>);
    if (k&) return 1ll*tmp*tmp%P*a%P;
    else return 1ll*tmp*tmp%P;
}
void inc(int &x,int y){x+=y;if (x>=P) x-=P;}
void DFT(int n,int *a,int p)
{
    for (int i=;i<n;i++) if (i<r[i]) swap(a[i],a[r[i]]);
    for (int i=;i<=n;i<<=)
    {
        int wn=ksm(p,(P-)/i);
        for (int j=;j<n;j+=i)
        {
            int w=;
            for (int k=j;k<j+(i>>);k++,w=1ll*w*wn%P)
            {
                int x=a[k],y=1ll*w*a[k+(i>>)]%P;
                a[k]=(x+y)%P;a[k+(i>>)]=(x-y+P)%P;
            }
        }
    }
}
int main()
{
    freopen("bzoj5093.in","r",stdin);
    freopen("bzoj5093.out","w",stdout);
    n=read(),k=read();
    ans=1ll*n*ksm(,1ll*(n-)*(n-)/%(P-))%P;
    n--;
    inv[]=;
    for (int i=;i<=max(,min(n,k));i++) inv[i]=(P-1ll*(P/i)*inv[P%i]%P)%P;
    a[]=ksm(,n);
    for (int i=;i<=min(n,k);i++)
    a[i]=1ll*a[i-]*inv[]%P*(n-i+)%P;
    v[]=;
    for (int i=;i<=min(n,k);i++)
    v[i]=(P-1ll*v[i-]*inv[i]%P)%P;
    s[]=;int facinv=;
    for (int i=;i<=min(n,k);i++)
    {
        facinv=1ll*facinv*inv[i]%P;
        s[i]=1ll*ksm(i,k)*facinv%P;
    }
    t=;while (t<=(min(n,k)<<)) t<<=;
    for (int i=;i<t;i++) r[i]=(r[i>>]>>)|(i&)*(t>>);
    DFT(t,s,),DFT(t,v,);
    for (int i=;i<t;i++) s[i]=1ll*s[i]*v[i]%P;
    DFT(t,s,inv[]);
    int p=ksm(t,P-);
    for (int i=;i<t;i++) s[i]=1ll*s[i]*p%P;
    for (int i=;i<=min(n,k);i++)
    inc(ans2,1ll*a[i]*s[i]%P);
    ans=1ll*ans*ans2%P;
    cout<<ans;
    fclose(stdin);fclose(stdout);
    return ;
}