leetcode647

class Solution {
public:
    bool ifHuiWen(bool DP[][],int i,int j){
        if(i>=j){
            return true;
        }
        else{
            return DP[i][j];
        }
    }

    int countSubstrings(string s) {
        int n=s.length();
        if(n==){
            return ;
        }
        int count=;
        bool DP[][];
        for(int i=;i<n;i++){
            DP[i][i]=true;
        }
        count+=n;
        for(int len=;len<n;len++){
            for(int i=;i<n-len;i++){
                int j=i+len;
                if(s[i]!=s[j]){
                    DP[i][j]=false;
                }
                else{
                    DP[i][j]=ifHuiWen(DP,i+,j-);
                    if(DP[i][j]){
                        count++;
                    }
                }
            }
        }

        return count;
    }
};

参考另外一个python的实现，解释的比较容易懂，代码思路和上面的是一样的。

 def countSubstrings(self, s):
     if not s:
         return 0

     n = len(s)
     table = [[False for x in range(n)] for y in range(n)]
     count = 0

     # Every isolated char is a palindrome
     for i in range(n):
         table[i][i] = True
         count += 1

     # Check for a window of size 2
     for i in range(n-1):
         if s[i] == s[i+1]:
             table[i][i+1] = True
             count += 1

     # Check windows of size 3 and more
     for k in range(3, n+1):
         for i in range(n-k+1):
             j = i+k-1
             if table[i+1][j-1] and s[i] == s[j]:
                 table[i][j] = True
                 count += 1

     return count

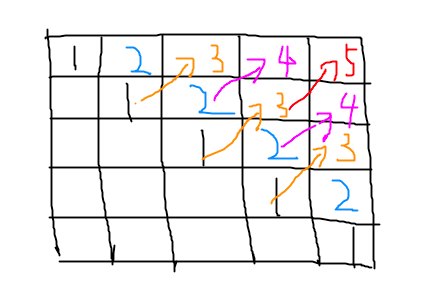
定义二维数组，table进行动态规划的记录。table[i][j]表示字符串s中，下标i到下标j之间的字符是否是回文字符，true表示：是回文；false表示：不是回文。

10～12行，第一次循环，将对角线上元素进行标记，全部标记为True，因为每一个单独字符都可以当作一个回文字符。

15～18行，第二次循环，将蓝色斜线进行标记，判断连续的两个字符是否相同，如果相同标记为True，否则标记为Flase。

12～26行，第三次循环，将剩下的橘色，品红和红色等进行标记，k的取值范围是从3到n，本例中n等于5。

k==3时，标记橘色，当其左下角位置为True，并且i元素和j元素字符相同（i与j相差2个位置，即i为0时j为2，i为1时j为3...以此类推）

k==4时，标记品红，当其左下角位置为True，并且i元素和j元素字符相同（i与j相差3个位置，即i为0时j为3，i为1时j为4...以此类推）

k==5时，标记红色，当期左下角位置为Ture，并且i元素和j元素字符相同（i与j相差4个位置，即i为0时j为4，以此类推）

这里的"左下角"表示：当前长度为k的子字符串，除去第0位和第k-1位后，"内部"的字符串是否是回文。

例如：s='abcbca'，假设此时k=3，则会分别依次判断：

abcbca —> abc，此时"左下角"表示的就是内部的字符b，而两头的a与c不相同，因此标记为False。

abcbca —> bcb，此时"左下角"表示的就是内部的字符c，而两头的b与b相同，因此标记为True。

abcbca —> cbc，此时"左下角"表示的就是内部的字符b，而两头的c与c相同，因此标记为True。

abcbca —> bca，此时"左下角"表示的就是内部的字符c，而两头的b与a不相同，因此标记为False。

在此上三角矩阵中（含对角线），所有标记为True的就是一个回文字符，True的个数就是所求。

参考：https://leetcode.com/problems/palindromic-substrings/discuss/128581/Easy-to-understand-Python-DP-solution