[CF1091D]New Year and the Permutation Concatenation

link

题目大意

给$n!$个$n$的排列，按字典序从小到大连成一条序列，例如$3$的情况为：$[1,2,3, 1,3,2, 2,1,3 ,2,3,1 ,3,1,2 ,3,2,1]$,问其中长度为$n$，且和为$sum=n\times (n+1)/2$的序列有多少个？

试题分析

对于合理的序列有两种情况，第一种是就是排列的，第二种就是前面$k$个与后面的$n-k$的一块组成。

对于第一种情况，答案只要$n$个，所以我们只考虑第二种情况。

当$n=3$时，$n\times n!=3!\times 3\text{=}18$

而直接生成的序列为$[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]$

而我们思考$next\_permutatin$是怎么判断下一个排列的，假设某一个序列长度为$n$，最长的递减的后缀长度$k$，那么它的下一个排列是这样产生的：那么它的下一个排列是这样产生的：与后$k$个数中比整个序列的第$n-k$个数大且最小的那个交换，然后将后$k$个数按从小到大排序。

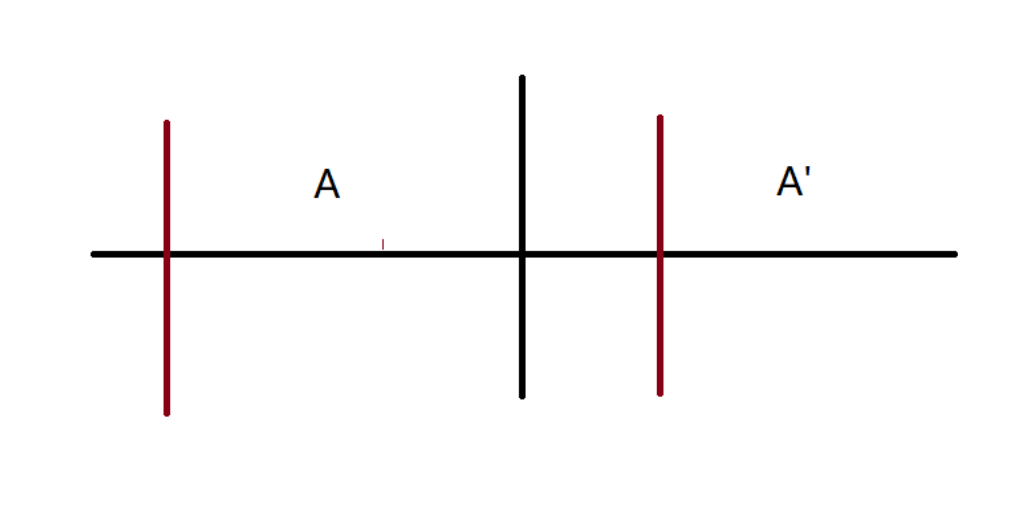
如图所示，若想要成为第二种情况，则$A$集合需等于$A’$集合。

而这时我们能确定$A$当前的一定不是递减的，所以问题可以转换成排除法当前序列末尾$k$个是按序递减的情况数。

举个例子:

$k=1$时，排除$[3,1,3],[2,2,1],[3,2,3],[1,3,1].[2,3,2]$

$k=2$时，排除$[(3,2),2],[(3,1),3]$

所以说我们现在只要求不行的方案数即可。

只要确定了前$k-x$个数，那么后面关于$x$的递减顺序是一定的。

所以当$k=x$时，排除方案数为$A_n^k$,但是最后一个是没有连接的，所以要$-1$，即为$A_n^k-1$

所以总方案数为$n\times n!-(n-1) - \sum_{k=1}^{n-1} (\frac{n!}{k!}-1)$.

整理的$n\times n!-\sum_{k=1}^{n-1} \frac{n!}{k!}$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define int long long
#define mod 998244353
using namespace std;
inline int read()
{
    int f=,ans=;char c;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){ans=ans*+c-'';c=getchar();}
    return ans*f;
}
const int N=;
int ans,n,fac[N],f[N];
signed main(){
    n=read();fac[]=;
    for(int i=;i<=n;i++) fac[i]=fac[i-]*i,fac[i]%=mod;
    f[n]=;
    for(int i=n-;i>=;i--) f[i]=f[i+]*(i+),f[i]%=mod;
    ans=n*fac[n];
    for(int i=;i<n;i++) ans=((ans-f[i])%mod+mod)%mod;
    printf("%d\n",ans);
}