2018.9.22 NOIP模拟赛

*注意：这套题目应版权方要求，不得公示题面。

从这里开始

• Problem A 妹子
• Problem B 旅程
• Problem C 老大

　　因为业务水平下滑太严重，去和高一考NOIP模拟，sad。。。

Problem A 妹子

题目大意

　　给定两个矩形，问一个能否将一个矩形放在另一个矩形里面。

　　先可以根据面积判断哪一个被放在里面，然后判断一下能不能直接放或者旋转90°放进去。

　　如果不行的话，接着考虑旋转。我们考虑这样↓放置小矩形。

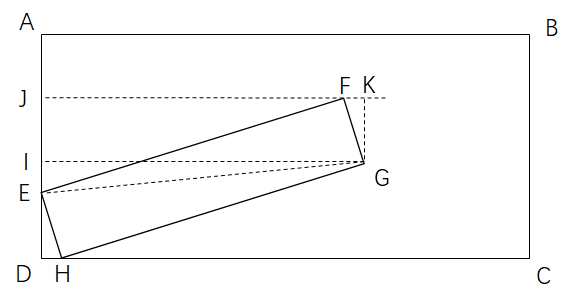
　　连接$EG$，作$GI\perp AD$于点$I$，$FJ\perp AD$与点$D$，$GK\perp JF$于点$G$。

　　考虑上下界$AB$和$CD$和左界$AD$的限制，暂时放开$BC$的限制，然后我们考虑最小化$GI$。

　　因为$GI^{2} = GE^2 - IE^2$，$GE$是定值，所以最小化$IG$等价于最大化$IE$。

　　易证四边形$JKGI$是矩形，所以$JI = KG$。易证$\angle FGK=\angle JFE=\angle DEH $。

　　再由$EH = FG,\angle EDH = \angle FKG = 90^{\circ}$，可得$\triangle EDH \cong  \triangle GKF$。

　　所以$JI = KG = ED$当$E$点向下移动的时候$DI$增大，$JI，ED$减小，所以当$DJ = AD$时，$IG$有最小值。

　　为了满足IG最小，我们这样放置矩形↓

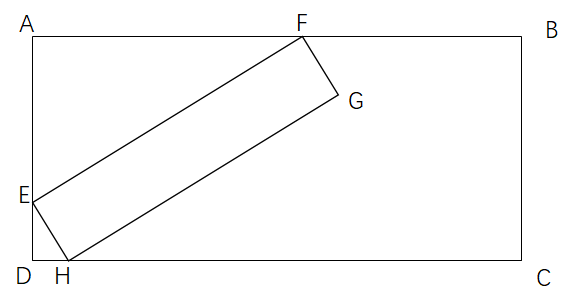
　　设$AF = x, \frac{EF}{EH} = k, w_{1} = EF, w_{2} = AD$。

　　因为$\left\{\begin{matrix}\angle AFE = \angle DEH\ \ \ \ \ \ \ \ \ \ \\\angle EAF = \angle EDH = 90^{\circ} \end{matrix}\right.$，所以$\triangle AFE \sim \triangle DEH$、

　　所以$ED = \frac{x}{k}, AE = \sqrt{w_{1}^{2} - x^{2}}$，然后有$k \cdot w_{2} - x = k\sqrt{w_{1}^{2} - x^{2}}$。

　　然后有：

$\left\{ \begin{matrix} k^{2} \cdot w_{2}^2 - 2x\cdot k\cdot w_{2} + x^2 = k^2w_{1}^{2} - k^2x^{2} \\ 0< x \leqslant w_{1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ k \cdot w_{2} - x > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix} \right.$

　　解一下，判断是否满足$CD$限制就行了。1

Code

 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <cmath>
 using namespace std;
 typedef bool boolean;

 int T;
 int w1, h1, w2, h2;
 double w;

 inline void init() {
     scanf("%d%d%d%d", &w1, &h1, &w2, &h2);
     if (w1 * h1 > w2 * h2) {
         swap(w1, w2);
         swap(h1, h2);
     }
 }

 boolean checkRoot(double x) {
      || x > w1)
         return false;
     double k = w1 * 1.0 / h1;
     double y = sqrt(w1 * w1 - x * x);
     return x + y / k <= h2;
 }

 boolean check() {
     double k = w1 * 1.0 / h1;
     ;
      * k * w2;
     double c = k * (w1 * w1 - w2 * w2);
      * a * c;
     )
         return false;
     double qd = sqrt(delta);
      * a), x2 = (-b + qd) / ( * a);
     return checkRoot(x1) || checkRoot(x2);
 }

 namespace old {

     boolean check() {
         if (w1 <= w2 && h1 <= h2)
             return true;
         if (w1 >= w2 && h1 >= h2)
             return true;
         return false;
     }

     inline boolean solve() {
         if (check()) {
             puts("Yes");
             return true;
         }

         swap(h1, w1);
         if (check()) {
             puts("Yes");
             return true;
         }

         swap(h1, w1);
         swap(h2, w2);
         if (check()) {
             puts("Yes");
             return true;
         }
         return false;
     }

 }

 inline void solve() {
     if (old::solve())
         return;
     if (check())
         puts("Yes");
     else {
         swap(h1, w1);
         if (check())
             puts("Yes");
         else
             puts("No");
     }
 }

 int main() {
     scanf("%d", &T);
     while (T--) {
         init();
         solve();
     }
     ;
 }

Problem A

Problem B 旅程

题目大意

　　给定$n$个点的带权有向完全图。要求支持删除一条边以及询问两点之间的最短路。

　　$1\leqslant n\leqslant 200, 1\leqslant m\leqslant 10^5$，删除操作不超过$200$次。

　　没有插入，倒着做，变成加。

　　然后考虑这条边带来的贡献，枚举一对点，用它来更新最短路。

　　时间复杂度$O(n^3 + m)$

Code

 #include <iostream>
 #include <cstdlib>
 #include <cstring>
 #include <cstdio>
 using namespace std;
 typedef bool boolean;

 ;
 );

 typedef class Operation {
     public:
         int type;
         int x, y;
         int data;

         Operation() {    }
         Operation(int type, int x, int y):type(type), x(x), y(y) {    }
 }Operation;

 int n, m;
 int d[N][N];
 int f[N][N];
 Operation *os;

 inline void init() {
     scanf("%d%d", &n, &m);
     ; i <= n; i++)
         ; j <= n; j++)
             scanf("%d", d[i] + j);
     os = )];
     , op, x, y; i <= m; i++) {
         scanf("%d%d%d", &op, &x, &y);
         os[i] = Operation(op, x, y);
         ) {
             os[i].data = d[x][y];
             d[x][y] = inf;
         }
     }
 }

 inline void solve() {
     memcpy(f, d, sizeof(f));
     ; i <= n; i++)
         f[i][i] = ;
     ; k <= n; k++)
         ; i <= n; i++)
             if (i ^ k)
                 ; j <= n; j++)
                     if ((j ^ k) && (j ^ i))
                         f[i][j] = min(f[i][k] + f[k][j], f[i][j]);

     for (int i = m; i; i--) {
         int op = os[i].type, x = os[i].x, y = os[i].y;
         ) {
             int data = os[i].data;
             if (data != inf) {
                 ; u <= n; u++)
                     ; v <= n; v++)
                         if (u ^ v)
                             f[u][v] = min(f[u][x] + data + f[y][v], f[u][v]);
             }
         } else {
             if (f[x][y] == inf)
                 os[i].data = -;
             else
                 os[i].data = f[x][y];
         }
     }

     ; i <= m; i++)
         )
             printf("%d\n", os[i].data);
 }

 int main() {
 //    freopen("journey.in", "r", stdin);
 //    freopen("journey.out", "w", stdout);
     init();
     solve();
     ;
 }

Problem B

Problem C 老大

题目大意

　　要求在树上找两个点，然后其他所有点到它们两个点的距离的最小值的最大值最小。

Solution 1 Binary search

　　二分答案$mid$，从最后一个点向上跳$mid$个点作为第一个选定点，然后把它的势力范围内的点都删掉，然后对剩下的点做一次，再判断是否有点剩余。

　　时间复杂度$O(n\log n)$

Solution 2 Dynamic programming

　　考虑只选一个点的时候，答案是最长链长度除以二向上取整。（根据最长链定义然后用反证法）。

　　选两个点就相当于每个点有个势力范围，分界边将树分成一个比较好看的子树，以及它的补。正反各一次求树上最长链dp就完了。

Code

 #include <algorithm>
 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <ctime>
 using namespace std;
 typedef bool boolean;

 typedef class Data {
     public:
         int mxlen;
         int mxdep;

         Data():mxlen(), mxdep() {    };
         Data(int mxlen, int mxdep):mxlen(mxlen), mxdep(mxdep) {    }

         Data operator + (Data b) {
             Data rt;
             rt.mxlen = max(mxlen, max(b.mxlen, b.mxdep + mxdep));
             rt.mxdep = max(mxdep, b.mxdep);
             return rt;
         }

         Data trans() {
             );
         }
 }Data;

 ;
 vector<int> *g;
 vector<int> *ts;
 Data *fu, *fd;

 Data *top;
 Data *pool;

 Data* alloc(int size) {
     Data* rt = top;
     top = top + size;
     return rt;
 }

 inline void init() {
     scanf("%d", &n);
     fu = )];
     fd = )];
     pool = ) + ];
     g = )];
     ts = )];
     top = pool;
     , u, v; i < n; i++) {
         scanf("%d%d", &u, &v);
         g[u].push_back(v);
         g[v].push_back(u);
     }
 //    cerr << clock() << endl;
 }

 void dp1(int p, int fa) {
     Data& f = fu[p];
     ; i < (signed) g[p].size(); i++) {
         int e = g[p][i];
         if (e == fa)
             continue;
         ts[p].push_back(e);
         dp1(e, p);
         f = f + fu[e].trans();
     }
 }

 void dp2(int p) {
     Data f = fd[p].trans() + Data(, );
     )
         f = Data(, );
     int s = (signed) ts[p].size();
     Data* pred = alloc(s + );
     Data* sufd = alloc(s + );
     Data d(, );
     ; i < s; i++) {
         int e = ts[p][i];
         d = d + fu[e].trans();
         pred[i] = d;
     }
     d = Data(, );
     ; ~i; i--) {
         int e = ts[p][i];
         d = d + fu[e].trans();
         sufd[i] = d;
     }

     ; i < s; i++) {
         int e = ts[p][i];
         fd[e] = f;
         if (i)
             fd[e] = fd[e] + pred[i - ];
         )
             fd[e] = fd[e] + sufd[i + ];
         dp2(e);
     }
 }

 int ceil2(int x) {
     ) >> ;
 }

 inline void solve() {
     dp1(, );
     dp2();
     ; i <= n; i++)
         res = min(res, max(ceil2(fd[i].mxlen), ceil2(fu[i].mxlen)));
     )
         res = ;
     printf("%d\n", res);
 }

 int main() {
 //    freopen("ob.in", "r", stdin);
 //    freopen("ob.out", "w", stdout);
     init();
     solve();
     ;
 }

Problem C