python实现线性规划

python工具包scipy linprog

函数格式

scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simplex', callback=None, options=None)

官方文档  https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html

实例

minmize:

       -7x1+7x2-2x3-x4-6x5

s.t.:

       3x1-x2+x3-2x4=-3

       2x1+x2+x4+x5=4

       -x1+3x2-3x4+x6=12

       xi>=0

程序代码：

import numpy as np
import matplotlib.pyplot as mpl
from scipy import optimize
c=np.array([-7,7,-2,-1,-6,0])
a=np.array([[3,-1,1,-2,0,0],[2,1,0,1,1,0],[-1,3,0,-3,0,1]])
b=np.array([-3,4,12])
 
res=optimize.linprog(c,A_eq=a,b_eq=b,bounds=((0,None),(0,None),(0,None),(0,None),(0,None),(0,None)))
print (res.x)
print (res.fun)

glpk求解

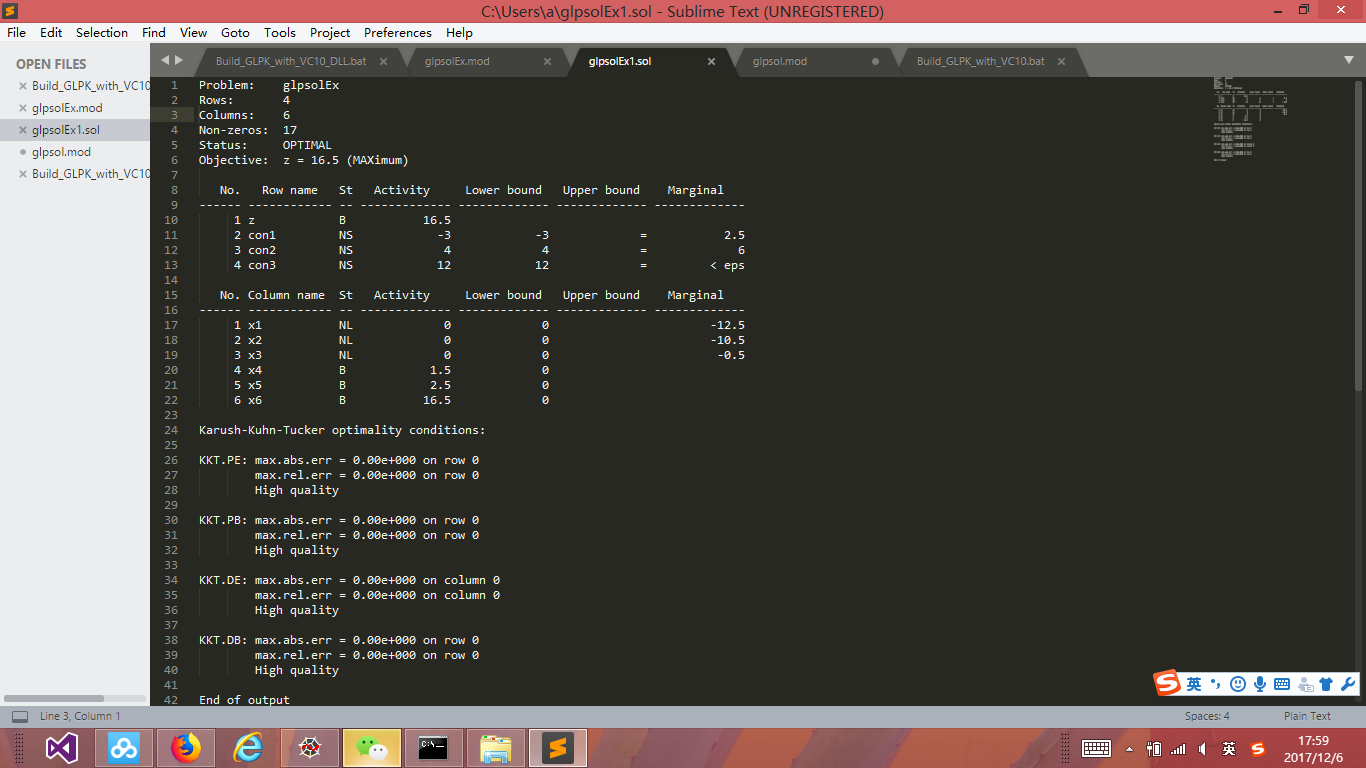
答案一致。