据说最近IMO中国队失利的一题

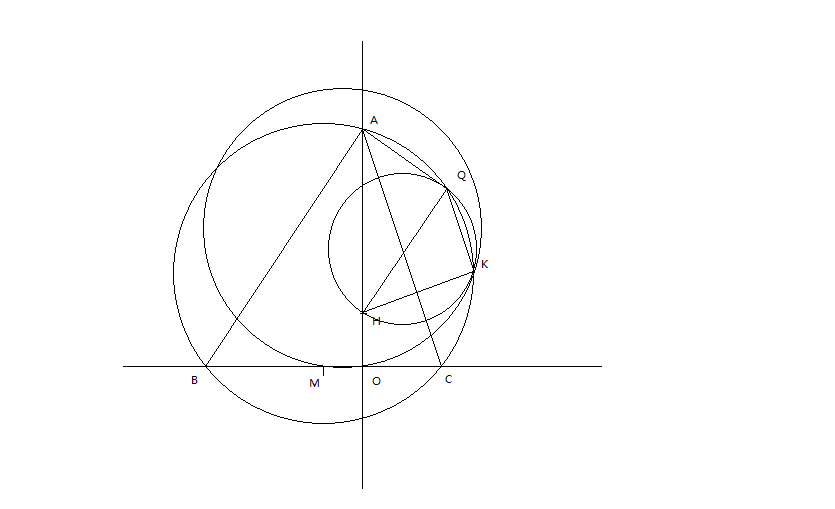
（图基于Microsoft PaintBrush技术构建）

平面几何是可以难得出蛆的。这道题难在多圆、高度非对称和具有一定复杂性。如图，对ABC，H是垂心，O是垂足，M是中点。QK在ABC外接圆上，均在图中小三角形上构成直角。现需要证明：三角形QHK的外接圆和MOK的的外接圆相切。

如果解析，估计也就做如图的坐标了，到求Q的坐标就可能需要解二元二次方程，K更不知道了。然后，没有然后了。

硬上，然后下去：

容易的点的坐标：
A（0,a)
B (-b,0)
C (c,0)
M ((c-b)/2, 0)
H (0, bc/a)

大圆圆心：( (c-b)/2, (a^2-bc)/2a )，半径：sqrt((a^2+b^2)*(a^2+c^2))/2a

三角形AQH的外接圆圆心：( 0, (a^2+bc)/2a)，半径：(a^2-bc)/2a

接下来是关键部分，解析分析上部的直角三角形组，从而求出Q和K的坐标。

可以发现用解析法，会出现多项式爆炸，奈么完结。

于是只有用上述解析中发现的一条平面几何定理（外接圆圆心到边的距离为垂心到对顶点的距离的一半）为突破口，发现这些点之间关联存在以下框架（这个框架非常似曾相识，也许以前看到过或者类似低阶题目）：

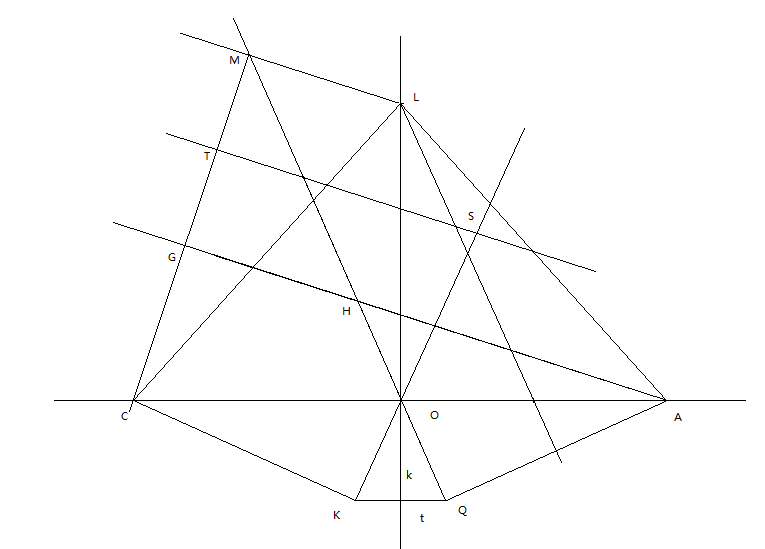
这其中L为原来三角形ABC的外接圆圆心，G为原图中垂足O，T为MG的中点。显然LKQ、OKQ、LCK、LQA为等腰三角形，形成关于y轴镜面对称结构，O处为原点可建立显然如图的直角坐标系。角OQA，OKC为直角，所以MQ和L向QA作的垂线平行。H和K关于x轴镜面对称。设Q的坐标为(-t, k)（于是显然K为(-t, -k)，H为(-t, k)），根据显然的相似关系A的坐标为(a, 0) = (k^2+t^2/t, 0)，L的坐标为(0, ka/2t)。

HA的方程易求，HA和y轴的交点坐标为ak/(a+t)。由上述关系，显然TS和y轴的交点为L和HA与y轴交点的中点，即：(k a^2 + 3a k t) / 4 t (a + t)。

LM和AH平行，AH被L对QA垂线平分，显然平分点和HML构成平行四边形，于是容易求出M的坐标为(-(a+t)/2, ka/2t+k/2)。

进一步，TS与GA平行，所以斜率也是-k/(a+t)，于是由TS的方程和OS的方程，得到S的坐标为( (a^2+3 a t) / 4(a+2t), k(a^2+3 a t) / 4 t (a+2t) )。

于是最终只要证明，SM = SK。（根据以上算式可证，用数值已经验证几组无误；但wolfram居然不给力，不能正确解出，可能要用自制程序来展开验证）