基于C语言的Q格式使用详解

用过DSP的应该都知道Q格式吧；

目录

• 1 前言
• 2 Q数据的表示
  • 2.1 范围和精度
  • 2.2 推导
• 3 Q数据的运算
  • 3.1 0x7FFF
  • 3.2 0x8000
  • 3.3 加法
  • 3.4 减法
  • 3.5 乘法
  • 3.6 除法
• 4 常见Q格式的数据范围
• 5 0x5f3759df
• 6 总结

1 前言

Q格式是二进制的定点数格式，相对于浮点数，Q格式指定了相应的小数位数和整数位数，在没有浮点运算的平台上，可以更快地对浮点数据进行处理，以及应用在需要恒定分辨率的程序中（浮点数的精度是会变化的）；需要注意的是Q格式是概念上小数定点，通过选择常规的二进制数整数位数和小数位数，从而达到所需要的数值范围和精度，这里可能有点抽象，下面继续看介绍。

2 Q数据的表示

2.1 范围和精度

定点数通常表示为\(Q_{m.n}\)，其中m为整数个数，n为小数个数，其中最高位位符号位并且以二进制补码的形式存储；

• 范围：\([-(2^{m-1})，2^{m-1}-2^{-n}]\)
• 精度：\(2^{-n}\)

无符号的用\(UQ_{m.n}\)表示；

• 范围：\([0，2^m-2^{-n}]\)
• 精度：\(2^{-n}\)

2.2 推导

无符号Q格式数据的推导

这里以一个16位无符号整数为例，\(UQ_{9.7}\)所能表示的最大数据的二进制形式如下图所示；

所以不难看出，\(UQ_{9.7}\)的范围大小和精度；

根据等比数列求和公式得到，整数域最大值如下：

\[Sumi = 2^8+2^7+2^6+2^5+2^4+2^3+2^2+2^1+2^0 = 2^9 -1
\]

小数域最大值如下：

\[Sumf = 2^{-1}+2^{-2}+2^{-3}+2^{-4}+2^{-5}+2^{-6}+2^{-7}=1-2^{-7}
\]

因此\(UQ_{9.7}\)的范围满足 \([0，2^9-2^{-7}]\)；

有符号Q格式数据的推导

这里以一个16位有符号整数为例，\(UQ_{9.7}\)所能表示的最大数据的二进制形式如下图所示；

所以不难求出，\(UQ_{9.7}\)的范围大小和精度；

根据等比数列求和公式得到，整数域最大值如下：

\[Sumi = 2^7+2^6+2^5+2^4+2^3+2^2+2^1+2^0 = 2^8 -1
\]

小数域最大值如下：

\[Sumf = 2^{-1}+2^{-2}+2^{-3}+2^{-4}+2^{-5}+2^{-6}+2^{-7}=1-2^{-7}
\]

因此\(Q_{9.7}\)最大能表示的数为： \(2^8-2^{-7}\)；

\(Q_{9.7}\)所能表示的最小数据的二进制形式如下图所示；

可以从图中看到，该数表示为\(-2^8\)；

补充一下：负数在计算机中是补码的形式存在的，补码=反码+1，符号位为1则表示为负数；

那么-4该如何表示呢？

以8 bit数据为例，如下所示；

原码：0B 0000 100

反码：0B 1111 011

补码：0B 1111 100

综上，可以得到有符号\(Q_{9.7}\)的范围是：\([-2^8，2^8-2^{-7}]\)

3 Q数据的运算

3.1 0x7FFF

最大数的十六进制为0x7FFF，如下图所示；

3.2 0x8000

最小数的十六进制为0X8000，如下图所示；

上述这两种情况，下面都会用到。

3.3 加法

加法和减法需要两个Q格式的数据定标相同，即\(Q_{m_1.n_1}\)和\(Q_{m_2.n_2}\)满足以下条件；

\[\begin{cases} m_1 = m_2 \\
n_1 = n_2
\end{cases}\]

int16_t q_add(int16_t a, int16_t b)
{
    return a + b;
}

上面的程序其实并不安全，在一般的DSP芯片具有防止溢出的指令，但是通常需要做一下溢出检测，具体如下所示；

int16_t q_add_sat(int16_t a, int16_t b)
{
    int16_t result;
    int32_t tmp;

    tmp = (int32_t)a + (int32_t)b;
    if (tmp > 0x7FFF)
        tmp = 0x7FFF;
    if (tmp < -1 * 0x8000)
        tmp = -1 * 0x8000;
    result = (int16_t)tmp;

    return result;
}

3.4 减法

类似于加法的操作，需要相同定标的两个Q格式数进行相减，但是不会存在溢出的情况；

//https://great.blog.csdn.net/
int16_t q_sub(int16_t a, int16_t b)
{
    return a - b;
}

3.5 乘法

乘法同样需要考虑溢出的问题，这里通过sat16函数，对溢出做了处理；

//https://great.blog.csdn.net/
// precomputed value:
#define K   (1 << (Q - 1))

// saturate to range of int16_t
int16_t sat16(int32_t x)
{
	if (x > 0x7FFF) return 0x7FFF;
	else if (x < -0x8000) return -0x8000;
	else return (int16_t)x;
}

int16_t q_mul(int16_t a, int16_t b)
{
    int16_t result;
    int32_t temp;

    temp = (int32_t)a * (int32_t)b; // result type is operand's type
    // Rounding; mid values are rounded up
    temp += K;
    // Correct by dividing by base and saturate result
    result = sat16(temp >> Q);

    return result;
}

3.6 除法

//https://great.blog.csdn.net/
int16_t q_div(int16_t a, int16_t b)
{
    /* pre-multiply by the base (Upscale to Q16 so that the result will be in Q8 format) */
    int32_t temp = (int32_t)a << Q;
    /* Rounding: mid values are rounded up (down for negative values). */
    /* OR compare most significant bits i.e. if (((temp >> 31) & 1) == ((b >> 15) & 1)) */
    if ((temp >= 0 && b >= 0) || (temp < 0 && b < 0)) {
        temp += b / 2;    /* OR shift 1 bit i.e. temp += (b >> 1); */
    } else {
        temp -= b / 2;    /* OR shift 1 bit i.e. temp -= (b >> 1); */
    }
    return (int16_t)(temp / b);
}

4 常见Q格式的数据范围

定点数\(X_q\)和浮点数\(X_f\)转换的关系满足以下公式：

\[\begin{cases}
X_q = (int)X_f*2^n \\
\\
X_f = (float)X_f*2^{-n}
\end{cases}\]

其中\(X_q\)为\(Q_{m.n}\)，m表示整数位数，n表示小数位数；

#include <stdio.h>
#include <stdint.h>
#include <math.h>

int main()
{
    // 0111 1111 1111 1111
    int16_t q_max = 32767; // 0x7FFF
    // 1000 0000 0000 0000
    int16_t q_min = -32768; // 0x8000
    float f_max = 0;
    float f_min = 0;
    printf("\r\n");
    for (int8_t i = 15; i>=0; i--) {
        f_max = (float)q_max / pow(2,i);
        f_min = (float)q_min / pow(2,i);

        printf("\t| Q %d | Q %d.%d| %f | %f |\r\n",
               i,(15-i),i,f_max,f_min);
    }

    return 0;
}

运行得到结果如下所示；

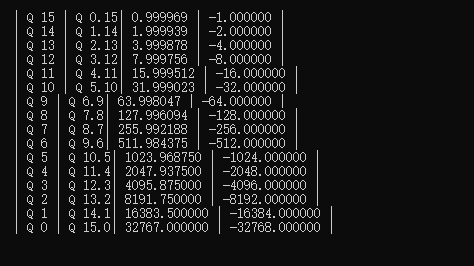
Q 格式	Qmn	Max	Min
Q 15	Q 0.15	0.999969	-1.000000
Q 14	Q 1.14	1.999939	-2.000000
Q 13	Q 2.13	3.999878	-4.000000
Q 12	Q 3.12	7.999756	-8.000000
Q 11	Q 4.11	15.999512	-16.000000
Q 10	Q 5.10	31.999023	-32.000000
Q 9	Q 6.9	63.998047	-64.000000
Q 8	Q 7.8	127.996094	-128.000000
Q 7	Q 8.7	255.992188	-256.000000
Q 6	Q 9.6	511.984375	-512.000000
Q 5	Q 10.5	1023.968750	-1024.000000
Q 4	Q 11.4	2047.937500	-2048.000000
Q 3	Q 12.3	4095.875000	-4096.000000
Q 2	Q 13.2	8191.750000	-8192.000000
Q 1	Q 14.1	16383.500000	-16384.000000
Q 0	Q 15.0	32767.000000	-32768.000000

5 0x5f3759df

Q格式虽然十分抽象，但是且看看这个数字0x5f3759df，感觉和Q格式有某种联系，它是雷神之锤3中的一个算法的魔数，毕竟游戏引擎需要充分考虑到效率，具体的由来可以看一下论文《Fast Inverse Square Root》，下面是源码中剥出来的快速平方根算法；

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y   = number;
	i   = * ( long * ) &y;   // evil floating point bit level hacking
	i   = 0x5f3759df - ( i >> 1 ); // what the fuck?
	y   = * ( float * ) &i;
	y   = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
	// y   = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed

	#ifndef Q3_VM
	#ifdef __linux__
		 assert( !isnan(y) ); // bk010122 - FPE?
	#endif
	#endif
	return y;
}

6 总结

本文介绍了Q格式的表示方式以及相应的运算，另外需要注意在Q格式运算的时候，两者定标必须相同，对于数据的溢出检测也要做相应的处理。

---

作者能力有限，文中难免有错误和纰漏之处，请大佬们不吝赐教

创作不易，如果本文帮到了您；

请帮忙点个赞