CF633(div.2)C. Powered Addition

题目描述

http://codeforces.com/contest/1339/problem/C

给定一个长度为 \(n\) 的无序数组，你可以在第 \(x\) 秒进行一次下面的操作。

• 从数组选取任意个数字（也可以一个都不选），为他们全部都加上 \(2^{x-1}\) 。

询问你最少可以用多少秒，使得数组非降序排列。

解题

最快策略

首先简化一下问题，假设操作变成：第 \(x\) 秒，可以选取任意个数字，为他们全部都加上 \(1\) 。分析一下在这个条件下，可以达到最少秒数的策略。

• 假设我们有一个分布如下图的不规则序列。

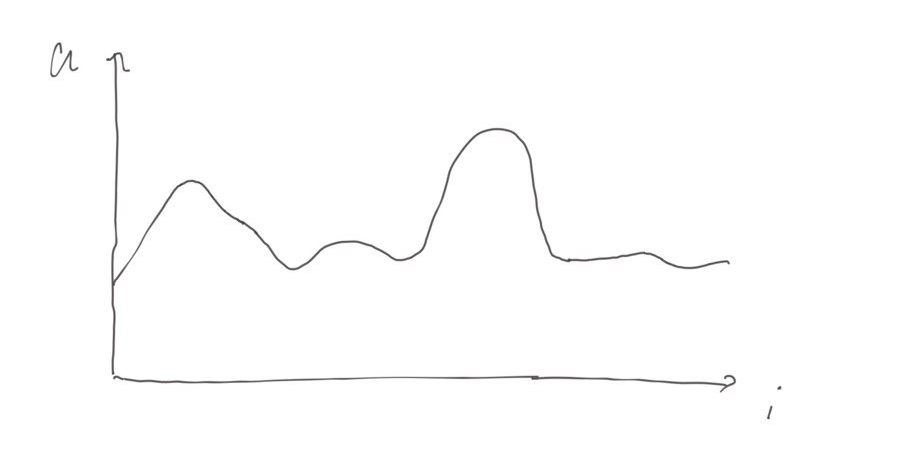
• 最快的让这个序列非降序排列的填充方案如图。

设对数字 \(a_i\) 加 \(1\) 的次数为 \(d_i\)，可以不难发现 \(d_i = max\{a_j|j\le i\} - a_i\) ，又因为每次 \(+1\) 操作是批量的，即每次可以选取多个 \(a_i\) 进行 \(+1\) 操作，所以最快策略的秒数花费 \(ans = max\{d_i|i\in[1,n]\}\) 。

最终解题

同理，设对数字 \(a_i\) 加 \(2^{x-1}\) 的操作次数为 \(d_i\)，

\[d_i = \left\{ \begin{array}{**lr**} sovle("max\{a_j|j\le i\} - a_i = \sum _{k=1}^{d_i}2^{k-1}")& ,max\{a_j|j\le i\} - a_i\gt 0\\\\ 0& ,max\{a_j|j\le i\} - a_i= 0\\ \end{array} \right.
\]

最后结果 \(ans = max\{d_i|i\in [1,n]\}\) 。

#include<bits/stdc++.h>
#define ll long long

#define fr(i,n) for(int i=0;i<n;i++)
#define frs(i,n,flag)   for(int i=0;i<n&&flag;i++)

#define frr(i,j,n) for(int i=j;i<n;i++)
#define r_frr(i,j,n) for(int i=n-1;i>=j;i--)

#define frrs(i,j,n,flag)    for(int i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag)    for(int i=n-1;i>=j&&flag;i--)

#define arend(i,n) ((i!=n-1)?" ":"\n")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end)    for(auto it = begin;it!=end;it++)  cout<<*it<<arend(it,end);
#define log_this(name,value)    cout<<name<<": "<<value<<endl;
#define e4 10004
#define e5 100005
#define e6 1000006
#define e7 10000007
#define e9 1000000000
#define INF 9999999
using namespace std;
int     to_int(string s)    {stringstream ss;ss<<s;int a;ss>>a;return a;}
string  to_str(double a)    {stringstream ss;ss<<a;return ss.str();}

ll a[1*e5];

int main(){

    cin.tie(0);
    //ios::sync_with_stdio(false);
    //cout<<setiosflags(ios::fixed)<<setprecision(0);

    //freopen("1.out","w",stdout);
    int t;
    while(cin>>t){
        while(t--){
            int n;
            cin>>n;
            fr(i,n){
                cin>>a[i];
            }
            ll pr = 0;
            ll maxa = a[0];
            fr(i,n-1){
                maxa = max(maxa,a[i+1]);
                pr = max(pr,maxa-a[i+1]);
            }
            ll x = 0;
            ll pw = 1;

            while(pr>0){
                pr -= pw;
                pw *= 2;
                x++;
            }

            cout<<x<<endl;
        }
    }

    return 0;
}