浅谈 PCA与SVD

前言

在用数据对模型进行训练时，通常会遇到维度过高，也就是数据的特征太多的问题，有时特征之间还存在一定的相关性，这时如果还使用原数据训练模型，模型的精度会大大下降，因此要降低数据的维度，同时新数据的特征之间还要保持线性无关，这样的方法称为主成分分析（Principal component analysis，PCA），新数据的特征称为主成分，得到主成分的方法有两种：直接对协方差矩阵进行特征值分解和对数据矩阵进行奇异值分解（SVD）。

一、主成分分析基本思想

  数据X由n个特征降维到k个特征，这k个特征保留最大信息（方差）。对原坐标系中的数据进行主成分分析等价于进行坐标系的旋转变化，将数据投影到新的坐标系下，新坐标系的第一坐标轴表示第一主成分，第二坐标轴表示第二主成分，以此类推。数据在每一轴上的坐标值的平方表示相应变量的方差，PCA的目标就是方差最大的变量，才能保留尽可能多的信息，因为方差越大，表示数据分散程度越大，所包含的信息也就越多。

二、PCA的基本步骤

• step1：对数据进行规范化（也称为标准化），因为涉及距离计算，因此要消除量纲的影响；
  
  这里的数据标准化采用z-score：X = X - mean(X) / std(X)
• step2：对数据X进行旋转变化（前言提到的两种方法）

三、数学推导

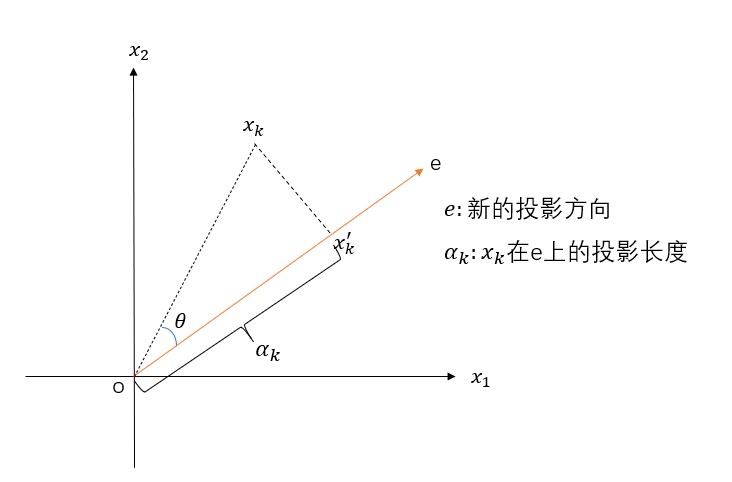
  假设X是m*n的矩阵，\(x_k\)是投影前的数据(k=1,2,…,n)，\(x_k^{'}\)是投影后的数据，e是新的坐标轴。投影长度\(α_k=e^tx_k\)，可以将\(e^t\)看成是cosθ，新数据\(x_k^{'}\)在新坐标轴e下的坐标为\(α_k e\)，表示从原点出发，沿着e方向走了\(α_k\)距离。根据方差最大的原则，即\(α_k\)要最大，由勾股定理\(\alpha_k^2+\left \| x_kx_k{'}\right \|^2=\left\|o x_k\right\|^2\)可知，当\(α_k\)最大时，\(\left\|x_kx_k^{'}\right\|^2\)要最小，因此转换成求\(\left\|x_kx_k^{'}\right\|^2\)最小，约束条件是\(\left\|e\right\|=1\)，数学表达式为：

\[\begin{cases}
min J(e)=\sum_{i=1}^n\left\|x_k^{'}-x_k\right\|^2\\
s.t. \left\|e\right\|=1
\end{cases}
\]

1. 完整的数学推导（结合第一部分的图）

\(min J(e)\\
=\sum_{i=1}^n\left\|x_k^{'}-x_k\right\|^2\\
=\sum_{i=1}^n\left\|\alpha_ke-x_k\right\|^2\\
=\sum_{i=1}^n\alpha_k^2\left\|e\right\|^2 - 2\sum_{i=1}^n\alpha_ke^tx_k + \sum_{i=1}^n\left\|x_k\right\|^2\\
=\sum_{i=1}^n\alpha_k^2-2\sum_{i=1}^n\alpha_k^2+\sum_{i=1}^n\left\|x_k\right\|^2\\
=-\sum_{i=1}^n\alpha_k^2+\sum_{i=1}^n\left\|x_k\right\|^2\\
=-\sum_{i=1}^ne^tx_kx_k^te+\sum_{i=1}^n\left\|x_k\right\|^2\)

要使\(-\sum_{i=1}^ne^tx_kx_k^te+\sum_{i=1}^n\left\|x_k\right\|^2\)最小，由于\(\sum_{i=1}^n\left\|x_k\right\|^2\)不包含e，因为转换为求\(\sum_{i=1}^ne^tx_kx_k^te\)的最大值，同时记\(S=\sum_{i=1}^nx_kx_k^t\)，实际上，S是协方差X的协方差矩阵，问题可转化为

\[\begin{cases}
max\quad e^tSe\\
s.t. \quad \left\|e\right\|=1
\end{cases}
\]

对于上述优化问题，可以用拉格朗日乘子法求解：\(u=e^tSe-\lambda(e^te-1),\frac{\partial u}{\partial e} = 2Se-2\lambda e=0\)，解得：\(Se = \lambda e\)

可以看出，满足条件的投影方向e(k个)是协方差矩阵S的前k大特征值对应的特征向量，因此PCA转化为求数据X的协方差矩阵的特征值，将特征值降序排序，对应的特征向量构成的矩阵就是所求的旋转矩阵

2. 求旋转矩阵

• 基于特征值求解
• 基于奇异值分解SVD

2.1 基于特征值求解

  就是一般的矩阵求特征值和特征向量的问题，此处不做详细介绍，需要注意的是，是对数据X的协方差矩阵\(X^TX\)求特征值和特征向量，前k个特征向量构成的矩阵P（此处默认P已经按照特征值的大小顺序进行排列，维度为n*k），那么新数据\(newX = X*P\),则newX由X的\(m*n\)变成\(m*k(k<n)\)，此时数据已经降低维度了。

2.2 基于SVD求解PCA

三、奇异值分解SVD

3.1 什么是奇异值分解

  对于任意的矩阵\(A\in\mathbb{R}^{m*n}\)，都可以将A分解成三个矩阵：

\[A=U\sum V^T,U\in\mathbb{R}^{m*m},\sum\in\mathbb{R}^{m*n},V\in\mathbb{R}^{n*n}
\]

并且U和V是正交阵，\(\sum\)是对角阵,即

\[UU^T=UU^{-1}=I,VV^T=VV^{-1}=I
\]

3.2 奇异值分解的几何解释

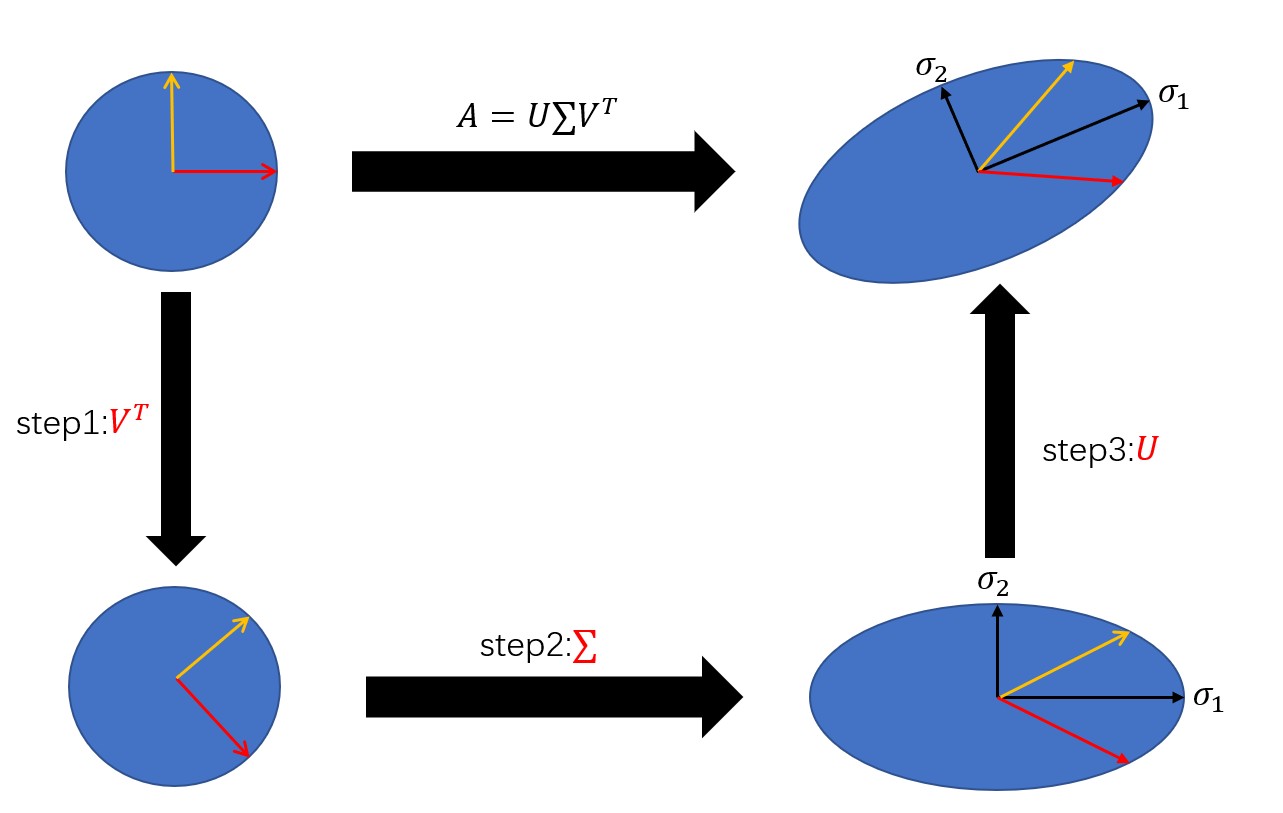
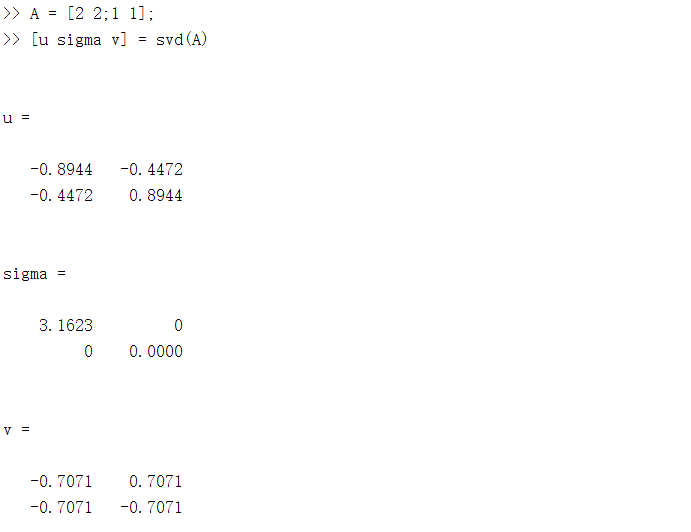
  本质上来说，奇异值分解是一个线性变换，对矩阵A进行奇异值分解可以看成是用一组正交基先进行旋转\((V^T e)\)，再进行坐标缩放\((\sum V^T e)\)，最后再进行坐标旋转\((U\sum V^T e)\)，经过这三步操作，正交基可以变换成A，下面是一个简单的例子，用MATLAB可以对任意矩阵进行奇异值分解，并且输出三个矩阵。

3.3 如何求解\(U,\sum,V^T\)

  (以下由于编辑问题，会出现几个\(\sum^T\)的T出现在\(\sum\)上面)

  对于任意的矩阵都能进行因子分解，这显然是SVD最大的好处，但关键是如何求解三个因子矩阵呢？

3.3.1 求解U

已知\(A=U\sum V^T\),则有

\[AA^T=(U\sum V^T)(U\sum V^T)^T=U\sum V^TV\sum^TU^T=U(\sum\sum^T)U^T
\]

又因为U是正交阵，因此有

\[U^T=U^{-1},AA^T=U(\sum\sum^T)U^{-1}
\]

左右各乘以\(U^{-1}\)，可以得到

\[AA^TU=U(\sum\sum^T)
\]

也就是U是矩阵\(AA^T\)的特征向量，\((\sum\sum^T)\)是特征值。

3.3.2 求解V

与求解U类似，通过\(AA^T\)来求解，最终可以得到

\[A^TAV=V(\sum^T\sum)
\]

也就是V是矩阵\(A^TA\)的特征向量，\((\sum^T\sum)\)是特征值

3.3.3 对角矩阵\(\sum\)

\(\sum\)里的元素成为奇异值，从3.3.1和3.3.2可以看出，对角矩阵\(\sum\)的奇异值是\(AA^T\)和\(A^TA\)的特征值的平方根，并且奇异值一定不小于0.以下是简单的证明：

令\(\lambda\)是\(A^TA\)的一个特征值，x是对应的特征向量，则

\[\left\|Ax\right\|^2=x^TA^TAx=\lambda x^Tx=\lambda\left\|x\right\|^2
\]

\[\lambda=\frac{\left\|Ax\right\|^2}{\left\|x\right\|^2}\geq0
\]

而奇异值\(\sigma\)是\(\lambda\)的平方根，因此也大于等于0.

3.3.4 SVD与PCA的关系

PCA的目标是求协方差矩阵\(X^TX\)的特征向量和特征值，而协方差矩阵的特征向量就是矩阵X奇异值分解后的右奇异向量V,用下图来说明PCA与SVD的关系



因此，经过PCA处理得到的新数据，其实就是对数据X做奇异值分解，然后乘上右奇异矩阵，或者左奇异矩阵乘上对角矩阵！

四、总结

  PCA是一种降维技术，主要用在特征提取。对于PCA，有两种方式：直接对数据的协方差矩阵进行特征向量的求解；对数据进行奇异值分解。实际上，后者会更优于前者。因为求解协方差矩阵的特征值以及特征向量时，有时会出现特征值为虚数，那么这时候算法会失效，而SVD求解出来的奇异值一定是非负数。除此之外，其实可以把PCA看做是对SVD的一种包装，如果实现了SVD，那么PCA也就实现了，而且更好的是，用SVD可以得到两个方向的PCA，而直接分解协方差矩阵，只能得到一个方向的PCA。